Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp H├¼nh hß╗Źc 8 B├Āi 1 Tß╗® gi├Īc sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng, giß║Żi b├Āi tß║Łp tß╗½ SGK H├¼nh hß╗Źc 8 Tß║Łp 1
-
B├Āi tß║Łp 1 trang 66 SGK To├Īn 8 Tß║Łp 1
T├¼m x ß╗¤ h├¼nh 5, h├¼nh 6:

-
B├Āi tß║Łp 2 trang 66 SGK To├Īn 8 Tß║Łp 1
G├│c kß╗ü b├╣ vß╗øi mß╗Öt g├│c cß╗¦a tß╗® gi├Īc gß╗Źi l├Ā g├│c ngo├Āi cß╗¦a tß╗® gi├Īc.
a) T├Łnh c├Īc g├│c ngo├Āi cß╗¦a tß╗® gi├Īc ß╗¤ h├¼nh 7a.
b) T├Łnh tß╗Ģng c├Īc g├│c ngo├Āi cß╗¦a tß╗® gi├Īc ß╗¤ h├¼nh 7b (tß║Īi mß╗Śi ─æß╗ēnh cß╗¦a tß╗® gi├Īc chß╗ē chß╗Źn mß╗Öt g├│c ngo├Āi): \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = ?\)
c) C├│ nhß║Łn x├®t g├¼ vß╗ü tß╗Ģng c├Īc g├│c ngo├Āi cß╗¦a tß╗® gi├Īc?
 ŌĆŗ
ŌĆŗ -
B├Āi tß║Łp 3 trang 67 SGK To├Īn 8 Tß║Łp 1
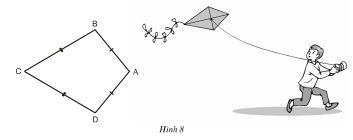
Ta gß╗Źi tß╗® gi├Īc ABCD tr├¬n h├¼nh 8 c├│ AB = AD, CB = CD l├Ā h├¼nh "c├Īi diß╗üu"
a) Chß╗®ng minh rß║▒ng AC l├Ā ─æŲ░ß╗Øng trung trß╗▒c cß╗¦a BD.
b) T├Łnh \(\widehat{B}, \widehat{D}\) biß║┐t rß║▒ng \(\widehat{A}= 100^0\) v├Ā \(\widehat{C}= 60^0\) .
-
B├Āi tß║Łp 4 trang 67 SGK To├Īn 8 Tß║Łp 1
Dß╗▒a v├Āo c├Īch vß║Į c├Īc tam gi├Īc ─æ├Ż hß╗Źc, h├Ży vß║Į lß║Īi c├Īc tß╗® gi├Īc ß╗¤ h├¼nh 9, h├¼nh 10 v├Āo vß╗¤.

-
B├Āi tß║Łp 5 trang 67 SGK To├Īn 8 Tß║Łp 1
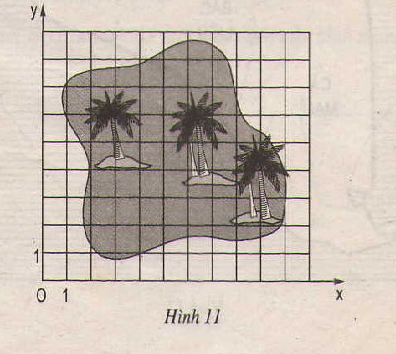
─Éß╗æ. ─Éß╗æ em t├¼m thß║źy vß╗ŗ tr├Ł cß╗¦a "kho b├Īu" tr├¬n h├¼nh 11, biß║┐t rß║▒ng kho b├Īu nß║▒m tß║Īi giao ─æiß╗ām c├Īc ─æŲ░ß╗Øng ch├®o cß╗¦a tß╗® gi├Īc ABCD, trong ─æ├│ c├Īc ─æß╗ēnh cß╗¦a tß╗® gi├Īc c├│ tß╗Źa ─æß╗Ö nhŲ░ sau: A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
-
B├Āi tß║Łp 1 trang 80 SBT To├Īn 8 Tß║Łp 1
T├Łnh tß╗Ģng c├Īc g├│c ngo├Āi cß╗¦a tß╗® gi├Īc (tß║Īi mß╗Śi ─æß╗ēnh cß╗¦a tß╗® gi├Īc chß╗ē chß╗Źn mß╗Öt g├│c ngo├Āi).
-
B├Āi tß║Łp 2 trang 80 SBT To├Īn 8 Tß║Łp 1
Tß╗® gi├Īc \(ABCD\) c├│ \(AB=BC, CD=DA.\)
\(a)\) Chß╗®ng minh rß║▒ng \(BD\) l├Ā ─æŲ░ß╗Øng trung trß╗▒c cß╗¦a \(AC\)
\(b)\) Cho biß║┐t \(\widehat B = {100^0},\widehat D = {70^0}\) t├Łnh \(\widehat A\) v├Ā \(\widehat C\).
-
B├Āi tß║Łp 3 trang 80 SBT To├Īn 8 Tß║Łp 1
Vß║Į lß║Īi tß╗® gi├Īc \(ABCD\) ß╗¤ h├¼nh \(1\) v├Āo vß╗¤ bß║▒ng c├Īch vß║Į hai tam gi├Īc.
-
B├Āi tß║Łp 4 trang 80 SBT To├Īn 8 Tß║Łp 1
T├Łnh c├Īc g├│c cß╗¦a tß╗® gi├Īc \(ABCD,\) biß║┐t rß║▒ng:
\(\widehat A:\widehat B:\widehat C:\widehat D = 1:2:3:4\)
-
B├Āi tß║Łp 5 trang 80 SBT To├Īn 8 Tß║Łp 1
Tß╗® gi├Īc \(ABCD\) c├│ \(\widehat A = {65^0},\widehat B = {117^0},\widehat C = {71^0}\). T├Łnh sß╗æ ─æo g├│c ngo├Āi tß║Īi ─æß╗ēnh \(D.\)
-
B├Āi tß║Łp 6 trang 80 SBT To├Īn 8 Tß║Łp 1
Chß╗®ng minh rß║▒ng c├Īc g├│c cß╗¦a mß╗Öt tß╗® gi├Īc kh├┤ng thß╗ā ─æß╗üu l├Ā g├│c nhß╗Źn, kh├┤ng thß╗ā ─æß╗üu l├Ā g├│c t├╣.
-
B├Āi tß║Łp 7 trang 80 SBT To├Īn 8 Tß║Łp 1
Cho tß╗® gi├Īc \(ABCD.\) Chß╗®ng minh rß║▒ng tß╗Ģng hai g├│c ngo├Āi tß║Īi c├Īc ─æß╗ēnh \(A\) v├Ā \(C\) bß║▒ng tß╗Ģng hai g├│c trong tß║Īi c├Īc ─æß╗ēnh \(B\) v├Ā \(D.\)
-
B├Āi tß║Łp 8 trang 80 SBT To├Īn 8 Tß║Łp 1
Tß╗® gi├Īc ABCD c├│ \(\widehat A = {110^0},\widehat B = {100^0}\). C├Īc tia ph├ón gi├Īc cß╗¦a c├Īc g├│c C v├Ā D cß║»t nhau ß╗¤ E. C├Īc ─æŲ░ß╗Øng ph├ón gi├Īc cß╗¦a c├Īc g├│c ngo├Āi tß║Īi c├Īc ─æß╗ēnh C v├Ā D cß║»t nhau ß╗¤ F. T├Łnh \(\widehat {CED},\widehat {CFD}\)
-
B├Āi tß║Łp 9 trang 80 SBT To├Īn 8 Tß║Łp 1
Chß╗®ng minh rß║▒ng trong mß╗Öt tß╗® gi├Īc, tß╗Ģng hai ─æŲ░ß╗Øng ch├®o lß╗øn hŲĪn tß╗Ģng hai cß║Īnh ─æß╗æi.
-
B├Āi tß║Łp 10 trang 80 SBT To├Īn 8 Tß║Łp 1
Chß╗®ng minh rß║▒ng trong mß╗Öt tß╗® gi├Īc, tß╗Ģng hai ─æŲ░ß╗Øng ch├®o lß╗øn hŲĪn nß╗Ła chu vi nhŲ░ng nhß╗Å hŲĪn chu vi cß╗¦a tß╗® gi├Īc ß║źy.
-
B├Āi tß║Łp 1.1 trang 81 SBT To├Īn 8 Tß║Łp 1
Tß╗® gi├Īc \(ABCD\) c├│ \(\widehat B =\widehat A+10^0,\)\(\widehat C=\widehat B+10^0,\) \(\widehat D=\widehat C+10^0\). Khß║│ng ─æß╗ŗnh n├Āo dŲ░ß╗øi ─æ├óy l├Ā ─æ├║ng?
\(A.\) \(\widehat A = {65^0}\)
\(B.\) \(\widehat B = {85^0}\)
\(C.\) \(\widehat C = {100^0}\)
\(D.\) \(\widehat D = {90^0}\)
-
B├Āi tß║Łp 1.2 trang 81 SBT To├Īn 8 Tß║Łp 1
Tß╗® gi├Īc \(ABCD\) c├│ \(\widehat C = {60^0},\)\(\widehat D = {80^0},\)\(\widehat A - \widehat B = {10^0}\). T├Łnh sß╗æ ─æo g├│c \(A\) v├Ā \(B.\)
-
B├Āi tß║Łp 1.3 trang 81 SBT To├Īn 8 Tß║Łp 1
Tß╗® gi├Īc \(ABCD\) c├│ chu vi \(66cm.\) T├Łnh ─æß╗Ö d├Āi \(AC,\) biß║┐t chu vi tam gi├Īc \(ABC\) bß║▒ng \(56cm,\) chu vi tam gi├Īc \(ACD\) bß║▒ng \(60cm.\)






