Giải bài 8 tr 80 sách BT Toán lớp 8 Tập 1
Tứ giác ABCD có \(\widehat A = {110^0},\widehat B = {100^0}\). Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính \(\widehat {CED},\widehat {CFD}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Tổng bốn góc của một tứ giác bằng \(360^o.\)
+) Hai tia phân giác của hai góc kề bù vuông góc với nhau.
Lời giải chi tiết
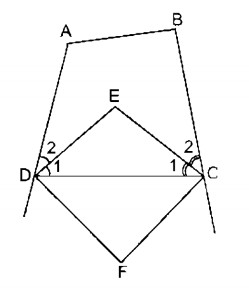
- Trong tứ giác ABCD, ta có:
\(\eqalign{
& \widehat A + \widehat B + \widehat C + \widehat D = {360^0} \cr
& \Rightarrow \widehat C + \widehat D = {360^0} - \left( {\widehat A + \widehat B} \right) \cr
& = {360^0} - \left( {{{110}^0} + {{100}^0}} \right) = {150^0} \cr
& {\widehat D_1} + {\widehat C_1} = {{\widehat C + \widehat D} \over 2} = {{{{150}^0}} \over 2} = {75^0} \cr} \)
- Trong ∆CED, ta có:
\(\widehat {CED} = {180^0} - \left( {{{\widehat C}_1} + {{\widehat D}_1}} \right) = {180^0} - {75^0} = {105^0}\)
DE ⊥ DF (tính chất tia phân giác của hai góc kề bù)
\(\Rightarrow \widehat {EDF} = {90^0}\)
CE ⊥ CF (tính chất tia phân giác của hai góc kề bù)
\( \Rightarrow \widehat {ECF} = {90^0}\)
Trong tứ giác CEDF, ta có:
\(\eqalign{
& \widehat {DEC} + \widehat {EDF} + \widehat {DFC} + \widehat {ECF} = {360^0} \cr
& \Rightarrow \widehat {DFC} = {360^0} - \left( {\widehat {DEC} + \widehat {EDF} + \widehat {ECF}} \right) \cr
& \widehat {DFC} = {360^0} - \left( {{{105}^0} + {{90}^0} + {{90}^0}} \right) = {75^0} \cr} \)
-- Mod Toán 8 HỌC247
-
Cho hình thoi PQRS. gọi A,B,C,D tương ứng là các trung điểm của các cạnh PQ, QS, RS, SP
bởi Thiên Mai
30/05/2019
cho hình thoi PQRS. gọi A,B,C,D tương ứng là các trung điểm của các cạnh PQ, QS,RS,SP. chứng minh rằng ABCD là một hình chữ nhật
cho hình vuông ABCD. gọi U, V, T , Z lần lượt là các trung điểm của các cạnh AB,BC,CD, DA. chứng minh rằng UVTZ là một hình vuông
Theo dõi (0) 1 Trả lời -
Cho hình bình hành ABCD có góc A =60°, AD=2AB
bởi Duy Quang
30/05/2019
Cho hình bình hành ABCD có góc A =60°,AD=2AB.Gọi M là trung điểm của AD,N là trung điểm của BC.a)CM tứ giác MNCD là hình thoi.b)Từ C kẻ đường thẳng vuông góc với MN tại E,cắt AB tại F.CM:E là trung điểm của CF.c)CM ∆MCF đều.d)CM ba điểm F,N,D thẳng hàng
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
Theo dõi (0) 1 Trả lời -
Chứng minh trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
bởi minh dương
08/04/2019
Chứng minh rằng trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Theo dõi (0) 1 Trả lời -
Chứng minh các góc của một tứ giác không thể đêu là góc nhọn, không thể đều là góc tù
bởi can tu
29/03/2019
Chứng minh rằng các góc của một tứ giác không thể đều là góc nhọn,không thể đều là góc tù
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB và AC ở D và E
a) Tìm các hình thang trong hình vẽ
b) Chứng minh rằng hình thang BDEC có một cạnh đáy bằng tổng hai cạnh bên
Theo dõi (0) 1 Trả lời -
Tam giác vuông có cạnh huyền bằng 12 cm, tính độ dài trung tuyến ứng với cạnh huyền
bởi thanh hằng
30/05/2019
1) Tam giác vuông có cạnh huyền bằng 12 cm. Hỏi trung tuyến ứng với cạnh huyền bằng bao nhiêu?
2) Cho góc xOy có số đo là 90 độ , điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox , vẽ điểm C đối xứng với A qua Oy
a) So sánh các độ dài OB và OC
b) Chứng minh 3 điểm B , O ,C thẳng hàngTheo dõi (0) 1 Trả lời -
Chứng minh trong 1 tứ giác tổng 2 đường chéo lớn hơn nửa chu vi và nhỏ hơn chu vi của tứ giác đó
bởi thu hảo
30/05/2019
CMR : trong 1 tứ giác tổng 2 đường chéo lớn hơn nửa chu vi và nhỏ hơn chu vi của tứ giác đó
Theo dõi (0) 1 Trả lời -
Cho tam giác nhọn ABC gọi H là trực tâm tam giác M là trung điểm BC. Gọi D là điểm đối xứng H qua M
bởi Trần Bảo Việt
30/05/2019
Cho tam giác nhọn ABC gọi H là trực tâm tam giác M là trung điểm BC. Gọi D là điểm đối xứng H qua M
Chứng minh các tam giác ABD, ACD vuông
Gọi I là trung điểm AD. Chứng minh IA=IB=IC=ID
Theo dõi (0) 1 Trả lời -
Cho hình bình hành ABCD. Gọi I là giao điểm của hai đường chéo AC và BD; M, N theo thứ tự là trung điểm của ID và IB
bởi Lê Nhật Minh
30/05/2019
Bài 1: Cho hình bình hành ABCD. Gọi I là giao điểm của hai đường chéo AC và BD; M, N theo thứ tự là trung điểm của ID và IB.
a, Cmr: AM//CN ( Câu này mk biết làm rùi!!! )
b, Kéo dài AM cắt BC tại E, chứng minh DE = \(\dfrac{1}{2}\)EC.
Giúp mk câu b nha!!!
Bài 2: Cho đoạn thẳng AB và C là một điểm bất kì trên đoạn thẳng đó. Trên cùng một nửa mặt phẳng bờ AB dựng các tam giác đều ACP và CBQ. Khi C chạy trên đoạn thẳng AB thì trung điểm E của đoạn thẳng PQ chạy trên đường nào?
Help me!!! Mk cần gấp!!!
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC cân tại B. Gọi M, N lần lượt là trung điểm của BA, BC. Đoạn thẳng AN và CM cắt nhau tại G
bởi Ngoc Nga
30/05/2019
Cho tam giác ABC cân tại B. Gọi M, N lần lượt là trung điểm của BA, BC. Đoạn thẳng AN và CM cắt nhau tại G.
a, Cm: MN là đường trung bình của tam giác ABC, G là điểm đặc biệt gì của tam giác ABC? Vì sao? ( Câu này mk biết làm rùi!!! )
b, Cm: AMNC là hình thang cân.
c, BG cắt AC tại K. Tứ giác AMNK là hình gì? Vì sao?
d, Tìm điều kiện của tam giác ABC để tứ giác AMNK là hình thoi.
Help me!!! Mk cần gấp!!!
Theo dõi (0) 1 Trả lời -
Tìm các đoạn đối xứng với đoạn thẳng AB qua d, đối xứng với đoạn thẳng AC qua c
bởi Xuan Xuan
30/05/2019
Cho \(\Delta ABC\) có AB < AC. Gọi d là đường trung trực của BC. Vẽ điểm D đối xứng với điểm A qua đường thẳng d.
a) Tìm các đoạn đối xứng với đoạn thẳng AB qua d, đối xứng với đoạn thẳng AC qua c.
b) Tứ giác ABCD là hình gì? Vì sao?
Theo dõi (0) 1 Trả lời -
Tính các góc của hình thang ABCD
bởi hoàng duy
30/05/2019
Cho hình thang \(\perp\)ABCD có \(\widehat{A}=\widehat{D}=90^o,AB=AD=2cm;DC=4cm\). Tính các góc của hình thang
Theo dõi (0) 1 Trả lời -
Cho góc xOy, điểm A nằm trong góc đó
bởi hi hi
30/05/2019
Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.
a) So sánh các độ dài OB và OC. ( Câu này mk biết làm rùi!!! )
b) Tính số đo góc xOy để B đối xứng với C qua O.
Help me!!! Giúp mk câu b nha các pạn!!!
Theo dõi (0) 1 Trả lời
