YOMEDIA
NONE
Trang chủ Toán 8

Bài tập 10 trang 80 SBT Toán 8 Tập 1

Lý thuyết5 Trắc nghiệm

18 BT SGK

240 FAQ

Giải bài 10 tr 80 sách BT Toán lớp 8 Tập 1

Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.

ATNETWORK

Hướng dẫn giải chi tiết

Hướng dẫn giải

Ta sử dụng kiến thức: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

Lời giải chi tiết

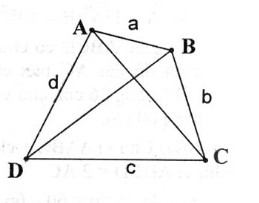
Đặt độ dài AB = a, BC = b, CD = c, AD = d

Gọi O là giao điểm hai đường chéo AC và BD

Trong ∆OAB, ta có:

OA + OA > a (bất đẳng thức tam giác)          (1)

Trong ∆OCD ta có:

Từ (1) và (2) suy ra:

OA + OB + OC + OD > a + c

Hay AC + BD > a + c  (*)

-Trong ∆OAD ta có: OA + OD > d (bất đẳng thức tam giác) (3)

-Trong ∆OBC ta có: OB + OC > b (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra: OA + OD + OB + OC > b + d

⇒ AC + BD > b + d (**)

Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d

\(⇒ AC + BD > {{a + b + c + d} \over 2}\)

-Trong ∆ABC ta có: AC < AB + BC =  a + b (bất đẳng thức tam giác)

-Trong ∆ADC ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)

Suy ra: 2AC < a + b + c + d

\(AC < {{a + b + c + d} \over 2}\)   (5)

-Trong ∆ABD ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)

-Trong ∆BCD ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)

Suy ra: 2BD < a + b + c + d

\(BD < {{a + b + c + d} \over 2}\)   (6)

Từ (5) và (6) suy ra: AC + BD < a + b + c + d

-- Mod Toán 8 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 10 trang 80 SBT Toán 8 Tập 1 HAY thì click chia sẻ 
YOMEDIA

Bài tập SGK khác

Bài tập 8 trang 80 SBT Toán 8 Tập 1

Bài tập 9 trang 80 SBT Toán 8 Tập 1

Bài tập 1.1 trang 81 SBT Toán 8 Tập 1

Bài tập 1.2 trang 81 SBT Toán 8 Tập 1

Bài tập 1.3 trang 81 SBT Toán 8 Tập 1

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 8

 

YOMEDIA
ATNETWORK
ON