Bài tập 24 trang 123 SGK Toán 8 Tập 1

Gọi \(h\) là chiều cao của tam giác cân có đáy là \(a\) và cạnh bên là \(b.\) 

Xét tam giác \(ABC\) cân tại \(A\) có \(AB=b, BC=a\) và chiều cao \(AH=h\). Ta tính diện tích tam giác \(ABC\).

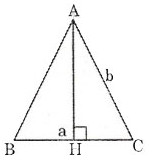
Vì \(\Delta ABC\) cân tại \(A\) (gt) nên \(AH\) vừa là đường cao vừa là đường trung tuyến (tính chất tam giác cân). Suy ra, \(H\) là trung điểm của \(BC\).

\( \Rightarrow BH = \dfrac{{BC}}{2} = \dfrac{a}{2}\)

Áp dụng định lý Pytago vào tam giác vuông \(ABH\) ta có: 

\(A{B^2} = A{H^2} + B{H^2}\)

\( \Rightarrow A{H^2} = A{B^2} - B{H^2}\)

\({h^2} = {b^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{4{b^2} - {a^2}}}{4} \)\(\Rightarrow h = \dfrac{{\sqrt {4{b^2} - {a^2}} }}{2}\)

Diện tích tam giác \(ABC\) là: 

\(S = \dfrac{1}{2}ah = \dfrac{1}{2}a.\dfrac{{\sqrt {4{b^2} - {a^2}} }}{2} \)\(= \dfrac{1}{4}a\sqrt {4{b^2} - {a^2}} .\)

-- Mod Toán 8 HỌC247