Bài tập 30 trang 160 SBT Toán 8 Tập 1
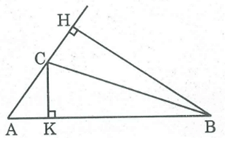
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
{S_{ABC}} = \frac{1}{2}.AB.CK\\
= \frac{1}{2}.AC.BH
\end{array}\)
Suy ra: AB.CK = AC.BH => \(\frac{{BH}}{{CK}} = \frac{{AB}}{{AC}}\)
Mà AB = 3AC (gt) => \(\frac{{BH}}{{CK}} = \frac{{3AC}}{{AC}}\) = 3
Vậy đường cao BH dài gấp 3 lần đường cao CK
-- Mod Toán 8 HỌC247
-


Cho tam giác đều ABC cạnh a và điểm M bất kì trong tam giác đó.gọi H,K,T ương ứng là hình chiếu vuông góc của điểm M trên BC,CA,AB.chứng minh rằng MH+MK+MT = \(\dfrac{a\sqrt{3}}{2}\).
Theo dõi (0) 1 Trả lời -


Cho tam giác đều ABC cạnh a và điểm M bất kì nằm trong tam giá đó. gọi H, K,T tương ứng là hình chiếu vuông góc của điểm M trên BC, CA,AB. Chứng minh rằng MH + Mk + Mt = \(\dfrac{a\sqrt{3}}{2}\)
Theo dõi (0) 1 Trả lời -


cho tam giác vuông ABC . Lấy AB , BC , CA làm cạnh dựng các hình vuông ACDE , BCGH và ABIK . C/m rằng diện tích BCGH=diện tích ACDE+ diện tích ABIK
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 28 trang 160 SBT Toán 8 Tập 1
Bài tập 29 trang 160 SBT Toán 8 Tập 1
Bài tập 31 trang 160 SBT Toán 8 Tập 1
Bài tập 32 trang 160 SBT Toán 8 Tập 1
Bài tập 3.2 trang 161 SBT Toán 8 Tập 1
Bài tập 3.3 trang 161 SBT Toán 8 Tập 1
Bài tập 25 trang 159 SBT Toán 8 Tập 1
Bài tập 26 trang 159 SBT Toán 8 Tập 1
Bài tập 27 trang 159 SBT Toán 8 Tập 1
Bài tập 28 trang 160 SBT Toán 8 Tập 1
Bài tập 29 trang 160 SBT Toán 8 Tập 1
Bài tập 30 trang 160 SBT Toán 8 Tập 1
Bài tập 31 trang 160 SBT Toán 8 Tập 1
Bài tập 3.1 trang 160 SBT Toán 8 Tập 1