Giải bài 3.2 tr 161 sách BT Toán lớp 8 Tập 1
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Gợi ý: Tổng diện tích của tam giác \(MBC,\,MCA,\,MAB\) bằng diện tích của tam giác \(ABC\)
Lời giải chi tiết
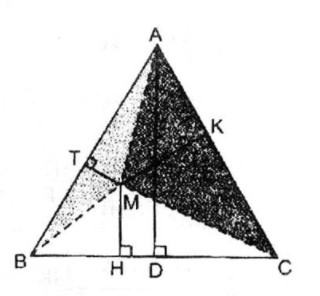
Giả sử \(∆ ABC\) đều có cạnh bằng \(a,\) kẻ đường cao \(AD,\) đặt \(AD = h\) không đổi.
Ta có:
\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}ah\\{S_{MAB}} = \dfrac{1}{2}MT.a\\{S_{MAC}} = \dfrac{1}{2}MK.a\\{S_{MBC}} = \dfrac{1}{2}MH.a\\{S_{ABC}} = {S_{MAB}} + {S_{MAC}} + {S_{MBC}}\\\dfrac{1}{2}ah = \dfrac{1}{2}MT.a + \dfrac{1}{2}MK.a \\+ \dfrac{1}{2}MH.a\\\dfrac{1}{2}ah = \dfrac{1}{2}a(MT + MK + MH)\\ \Rightarrow MT + MK + MH = h\end{array}\)
\( \Rightarrow MT + MK + MH = h\) không đổi
Vậy tổng \(MT + MK + MH\) không phụ thuộc vào điểm \(M.\)
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





