Bài tập 16 trang 67 SGK Toán 8 Tập 2

18 BT SGK

Giải bài 16 tr 67 sách GK Toán 8 Tập 2

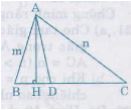
Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng \(\frac{m}{n}\).

Hình học 8 Bài 3 Trắc nghiệm Hình học 8 Bài 3 Giải bài tập Hình học 8 Bài 3

Hướng dẫn giải chi tiết

Kẻ \(AH ⊥ BC\)

Ta có:

\({S_{ABD}} = \dfrac{1}{2}AH.BD\)

\({S_{ACD}} = \dfrac{1}{2}AH.DC\)

\(\Rightarrow \dfrac{S_{ABD}}{S_{ACD}} = \dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC} = \dfrac{BD}{DC}\)

Mặt khác: \(AD\) là đường phân giác của \(∆ABC\) (gt)

\(\Rightarrow \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\) (tính chất đường phân giác của tam giác)

Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\) (điều phải chứng minh).

-- Mod Toán 8 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 16 trang 67 SGK Toán 8 Tập 2 HAY thì click chia sẻ

YOMEDIA

Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N. Chứng minh M đối xứng với N qua O.

bởi Bích Lê Hoàng 02/12/2021

Câu 18: (1,5 điểm) Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.

a. Chứng minh M đối xứng với N qua O.

b, Chứng tỏ rằng tứ giác AMCN là hình bình hành.

Theo dõi (1) 1 Trả lời
Tính độ dài đường phân giác BD?

bởi đoàn chung 07/07/2020

tam giác abc có ab=ac=20cm ;bc=5cm .tính độ dài đg phân giác bd

Theo dõi (0) 8 Trả lời
Chứng minh tam giác ABE đồng dạng với tam giác ACF.?

bởi Nguyễn Thư 23/06/2020

Cho tam giác ABC nhọn (AB < AC). Có hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh tam giác ABE đồng dạng với tam giác ACF.

b) Chứng minh tam giác AFE đồng dạng với tam giác ACB.

c) Tia phân giác của góc ABE cắt tia phân giác của góc ACF tại K, gọi I, J lần lượt là trung điểm của AH và BC. Chứng minh I, K, J thẳng hàng.

Theo dõi (0) 1 Trả lời
Chứng minh \(\frac{{MD}}{{ME}} = \frac{{NC}}{{NB}}\)?

bởi Linh Lam 14/06/2020

Giải giúp em với

Câu c ấy ạ!

Giải thích các bước làm và tại sao làm vậy giúp em nha giúp em nha.cảm ơn

Theo dõi (1) 0 Trả lời
Chứng minh rằng \(\left( {a + b} \right)\left( {{a^2} + {b^2} - {c^2}} \right) = 2{a^2}b\)?

bởi thuhuyen 14/06/2020

Giải giup e bài này với ạ

Theo dõi (0) 0 Trả lời