Bài tập 23 trang 88 SBT Toán 8 Tập 2

Hướng dẫn giải

Sử dụng:

- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.

- Định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.

- Tính chất:  \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)

Lời giải chi tiết

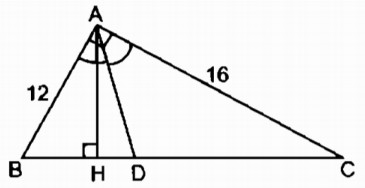
a) Áp dụng định lí Py-ta-go vào tam giác vuông \(ABC\), ta có: 

\(B{C^2} = A{B^2} + A{C^2} = {12^2} + {16^2} \)\(\,= 400\)

\( \Rightarrow BC = 20 \;(cm)\).

Vì \(AD\) là đường phân giác của \(\widehat {BAC}\) nên ta có:

\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác của tam giác)

Áp dụng tính chất mở rộng của tỉ lệ thức ta có:

\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\)

\( \Rightarrow \displaystyle {{DB} \over {DB + DC}} = {{AB} \over {AB + AC}}\)

\( \Rightarrow \displaystyle {{DB} \over {BC}} = {{AB} \over {AB + AC}}\)

\( \Rightarrow \displaystyle  DB = {{BC.AB} \over {AB + AC}} = {{20.12} \over {12 + 16}} \)\(\, \displaystyle = {{60} \over 7}\) (cm)

Vậy \(DC = BC - DB = \displaystyle 20 - {{60} \over 7} = {{80} \over 7}\) (cm)

b) Ta có \(\displaystyle {S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}AH.BC\)

\( \Rightarrow AB.AC = AH.BC\)

\( \Rightarrow \displaystyle  AH = {{AB.AC} \over {BC}} = {{12.16} \over {20}} = 9,6\)  (cm)

Áp dụng định lí Py-ta-go vào tam giác vuông \(AHB\), ta có:

\(A{B^2} = A{H^2} + H{B^2}\)

\( \Rightarrow  H{B^2} = A{B^2} - A{H^2}\)\(\, = {12^2} - {\left( {9,6} \right)^2} = 51,84 \)

\(\Rightarrow HB = 7,2\;(cm)  \)

Vậy \(\displaystyle  HD = BD - HB = {{60} \over 7} - 7,2 \)\(\,\approx 1,37\; (cm)\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(AHD\), ta có:

\(A{D^2} = A{H^2} + H{D^2} \)\(\,= {\left( {9,6} \right)^2} + {\left( {1,37} \right)^2} \)\(\,= 94,0369\)

\( \Rightarrow  AD ≈ 9,7\; (cm)\).

-- Mod Toán 8 HỌC247