Giải bài 24 trang 88 SBT Toán 8 Tập 2
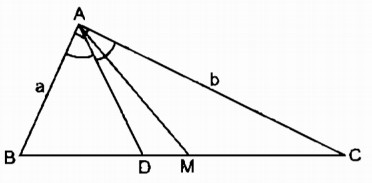
Tam giác vuông ABC có$\widehat A = 90^\circ $, AB = a (cm), AC = b (cm), (a < b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC) (h.20).
a. Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b.
b. Hãy tính các đoạn thẳng trên đây chính xác đến chữ số thập phân thứ hai khi biết a = 4,15cm, b = 7,25cm.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
- Tính chất: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Lời giải chi tiết
a) Áp dụng định lí Py-ta-go vào tam giác vuông \(ABC\), ta có:
\(B{C^2} = A{B^2} + A{C^2} = {a^2} + {b^2}\)
\( \Rightarrow BC = \sqrt {{a^2} + {b^2}} \)
Ta có: \( \displaystyle AM = BM = {1 \over 2}BC\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
\( \displaystyle \Rightarrow AM = {1 \over 2}\sqrt {{a^2} + {b^2}} \)
Vì \(AD\) là đường phân giác của \(\widehat {BAC}\) nên theo tính chất đường phân giác của tam giác ta có:
\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\)
Từ đó, ta có:
\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\)
\( \Rightarrow \displaystyle {{DB} \over {DB + DC}} = {{AB} \over {AB + AC}}\)
\( \Rightarrow \displaystyle {{DB} \over {BC}} = {{AB} \over {AB + AC}}\)
\( \Rightarrow DB = \dfrac{{AB.BC}}{{AB + AC}} = \dfrac{{a\sqrt {{a^2} + {b^2}} }}{{a + b}}\)
Vậy \(DC = BC - DB \)\(\,=\displaystyle \sqrt {{a^2} + {b^2}} - {{a\sqrt {{a^2} + {b^2}} } \over {a + b}}\)\(\,\displaystyle = {{b\sqrt {{a^2} + {b^2}} } \over {a + b}}\)
\(\eqalign{ & DM = BM - BD \cr & = {1 \over 2}\sqrt {{a^2} + {b^2}} - {{a\sqrt {{a^2} + {b^2}} } \over {a + b}} \cr} \)
\(\begin{array}{l}
= \dfrac{{\left( {a + b} \right)\sqrt {{a^2} + {b^2}} - 2a\sqrt {{a^2} + {b^2}} }}{{2\left( {a + b} \right)}}\\
= \dfrac{{\sqrt {{a^2} + {b^2}} \left( {a + b - 2a} \right)}}{{2\left( {a + b} \right)}}\\
= \dfrac{{\left( {b - a} \right)\sqrt {{a^2} + {b^2}} }}{{2\left( {a + b} \right)}}
\end{array}\)
b) Với \(a = 4,15\;cm; b= 7,25 \;cm\), ta tính được:
\( BC = \sqrt {{{\left( {4,15} \right)}^2} + {{\left( {7,25} \right)}^2}}\)\(\; \approx 8,35(cm) \)
\(\displaystyle BD = {{4,15\sqrt {{{\left( {4,15} \right)}^2} + {{\left( {7,25} \right)}^2}} } \over {4,15 + 7,25}} \)\(\,\approx 3,04(cm) \)
\(DC = \dfrac{{b\sqrt {{a^2} + {b^2}} }}{{a + b}}\approx 5,31(cm) ;\)
\(\displaystyle AM = {1 \over 2}\sqrt {{a^2} + {b^2}} \approx 4,18(cm) ;\)
\(\,DM= \dfrac{{\left( {b - a} \right)\sqrt {{a^2} + {b^2}} }}{{2\left( {a + b} \right)}} \approx 1,14(cm) .\
-- Mod Toán 8 HỌC247
-


Bài 3.1 trang 89 sách bài tập toán 8 tập 2
bởi Nguyễn Quang Thanh Tú
 29/09/2018
Bài 3.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 89)
29/09/2018
Bài 3.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 89)Tam giác ABC vuông tại A có đường phân giác AD. Biết rằng độ dài của các cạnh góc vuông AB = 3,75 cm, AC = 4,5 cm (h.bs.2)
Hãy chọn kết quả đúng (tính chính xác đến hai chữ số thập phân)
1) Độ dài của đoạn thẳng BD là :
(A) 18,58 (B) 2,66
(C) 2,65 (D) 3,25
2) Độ dài của đoạn thẳng CD là :
(A) 27,13 (B) 2,68
(C) 3,20 (D) 3,15
Theo dõi (0) 1 Trả lời -


Bài 24 trang 88 sách bài tập toán 8 tập 2
bởi Mai Thuy
 31/05/2019
Bài 24 (Sách bài tập - tập 2 - trang 88)
31/05/2019
Bài 24 (Sách bài tập - tập 2 - trang 88)Tam giác vuông ABC có \(\widehat{A}=90^0\), AB = a (cm), AC = b (cm), (a <b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC) (h.20)
a) Tính độ dài các đoạn thẳng BC, BDm DCm AM và DM theo a, b
b) Hãy tính các đọa thẳng trên đây chính xác đến chữ số thập phân thứ hai khi biết a = 4,15 cm, b = 7,25 cm
Theo dõi (0) 1 Trả lời -


Bài 22 trang 88 sách bài tập toán 8 tập 2
bởi bach dang
 29/09/2018
Bài 22 (Sách bài tập - tập 2 - trang 88)
29/09/2018
Bài 22 (Sách bài tập - tập 2 - trang 88)Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15 cm, BC = 10 cm (h.19)
a) Tính AD, DC
b) Đường vuông góc với BD tại B cắt đường thẳng AC kéo dài tại E. Tính EC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB = 9cm , AC = 12cm, BC =15cm, phân giác góc B căt AC tại D
bởi can chu
 13/09/2018
13/09/2018
Cho tam giác ABC có AB = 9cm ; AC = 12cm ; BC =15cm, phân giác góc B căt AC tại D và cắt đg cao AH tại I
a) Tính AD = ? ; DC = ?
b) C/m : IH . BD = IA .IB
Mn ưi giúp mk vs nakkk
Theo dõi (0) 1 Trả lời





