Giải bài 17 trang 87 SBT Toán 8 Tập 2
Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt BC tại D (h.14)
a. Tính độ dài đoạn thẳng DB và DC
b. Tính tỉ số diện tích của hai tam giác ABD và ACD.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Tính chất: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Lời giải chi tiết
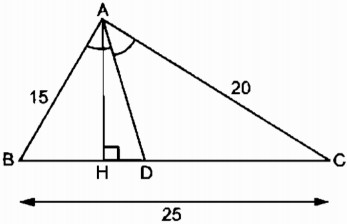
a) Áp dụng tính chất đường phân giác vào \(\Delta ABC\), đường phân giác \(AD\) ta có:
\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\)
\(\displaystyle \Rightarrow {{DB} \over {DC}} = {{15} \over {20}}=\dfrac{3}{4}\)
Ta có:
\(\displaystyle {{DB} \over {DC}} = \dfrac{3}{4}\)
\( \displaystyle \Rightarrow {{DB} \over {DB + DC}} = \dfrac{3}{{3 + 4}}\)
\(\displaystyle \Rightarrow {{DB} \over {BC}} = \dfrac{3}{7}\)
\( \displaystyle \Rightarrow DB = \dfrac{3}{7}.BC = \dfrac{3}{7}.25 = {{75} \over 7}\) (cm)
Từ đó: \(DC=BC-BD\)\( \displaystyle =25- {{75} \over 7}={{100} \over 7}\) (cm)
b) Kẻ \(AH ⊥ BC\)
Ta có: \(\displaystyle {S_{ABD}} = {1 \over 2}AH.BD;\) \(\displaystyle {S_{ADC}} = {1 \over 2}AH.DC\)
\(\Rightarrow\displaystyle {{{S_{ABD}}} \over {{S_{ADC}}}} = {\displaystyle{{1 \over 2}AH.BD} \over {\displaystyle{1 \over 2}AH.DC}} = {{BD} \over {DC}}\)
Mà \(\displaystyle {{DB} \over {DC}} = {{15} \over {20}} = {3 \over 4}\) (chứng minh trên )
Vậy \(\displaystyle {{{S_{ABD}}} \over {{S_{ADC}}}} = {3 \over 4}\).
-- Mod Toán 8 HỌC247
-


cho hình chứ nhật ABCD có AB=8cm, BC=6cm. Vẽ đường cao AH của \(\Delta\)ADB
a) tính DB
b) chứng minh \(\Delta\)ADH ∼ \(\Delta\)ADB
c) chứng minh AD2 = DH.DB
d) chứng minh \(\Delta AHB\sim\Delta BCD\)
e) tính độ dài đoạn thẳng DH, AH
Bài 2
cho\(\Delta ABC\) vuông tại A, có AB=6cm, AC=8cm. Vẽ đường cao AH
a) tính BC
b) chứng minh \(\Delta ABC\sim\Delta AHB\)
c) chứng minh AB2 =BH.BC. Tính BH, HC
d) vẽ phân giác AD của góc A( D\(\in\)BC) .TÍnh DB
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC vuông
bởi Nguyễn Sơn Ca
 31/05/2019
31/05/2019
De bai : Cho tam giac ABC co AB=9 cm,BC=12 cm,BC=15 cm
a,C/m tam giac ABC vuong
b,Duong phan giac cua goc B cat AC tai D . Tinh AD,DC
c,Duong cao AH cat BD tai I. Chung minh IH.BD=IA.IB
d,Chung minh tam giac AID can
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác DECđồng dạng tam giác ABC
bởi Lan Anh
 31/05/2019
31/05/2019
Cho ∆ABC có 2 đg cao AD và BE. Chứng minh:
a) ∆DEC ~ ∆ABC
b) ∆ADC~∆ BEC
Theo dõi (0) 1 Trả lời -


Chứng minh ba điểm A,M,N thẳng hàng biết trrên cạnh BC lấy điểm M sao cho BM=2cm
bởi thanh duy
 31/05/2019
31/05/2019
Cho tam giác ABC.Trên cạnh BC lấy điểm M sao cho BM=2CM.Trên tia AC lấy điểm D sao cho C là trung điểm của AD và gọi N là trung điểm của BD.Chứng minh rằng ba điểm A,M,N thẳng hàng
Theo dõi (0) 1 Trả lời -


Tính (3- √5) . √(3+√5) + ( 3+ √5)
bởi Nguyễn Hoài Thương
 31/05/2019
31/05/2019
(3- √5) . √(3+√5) + ( 3+ √5). √(3-√5)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 21 trang 68 SGK Toán 8 Tập 2
Bài tập 22 trang 68 SGK Toán 8 Tập 2
Bài tập 18 trang 87 SBT Toán 8 Tập 2
Bài tập 19 trang 87 SBT Toán 8 Tập 2
Bài tập 20 trang 87 SBT Toán 8 Tập 2
Bài tập 21 trang 88 SBT Toán 8 Tập 2
Bài tập 22 trang 88 SBT Toán 8 Tập 2
Bài tập 23 trang 88 SBT Toán 8 Tập 2
Bài tập 24 trang 88 SBT Toán 8 Tập 2





