Giải bài 21 trang 88 SBT Toán 8 Tập 2
Cho tam giác vuông ABC (\(\widehat A = {90^0}\)), AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thẳng qua D và song song với AB, cắt AC tại E
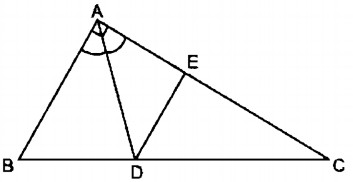
a. Tính độ dài các đoạn thẳng BD, DC và DE.
b. Tính diện tích tam giác ABD và diện tích tam giác ACD.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Hệ quả của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
- Tính chất: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Lời giải chi tiết
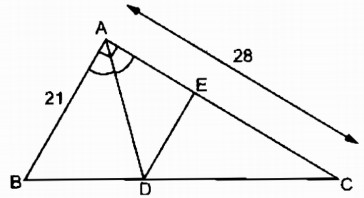
a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {21^2} + {28^2} = 1225\)
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của \(\widehat {BAC}\) nên:
\({{BD} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác )
Suy ra: \({{BD} \over {BD + DC}} = {{AB} \over {AB + AC}}\)
hay \({{BD} \over {BC}} = {{AB} \over {AB + AC}}\)
Suy ra: \(BD = {{BC.AB} \over {AB + AC}} = {{35.21} \over {21 + 28}} = 15\) (cm)
Vậy DC = BC – BD = 35 – 15 = 20 (cm)
Trong tam giác ABC ta có: DE // AB
Suy ra: \({{DC} \over {BC}} = {{DE} \over {AB}}\) (Hệ quả định lí Ta-lét )
Suy ra: \(DE = {{DC.AB} \over {BC}} = {{20.21} \over {35}} = 12\) (cm)
b. Ta có: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.21.28 = 294(c{m^2})\)
Vì ∆ ABC và ∆ ADB có chung đường cao kẻ từ đỉnh A nên:
\(\eqalign{ & {{{S_{ADB}}} \over {{S_{ABC}}}} = {{BD} \over {BC}} = {{15} \over {35}} = {3 \over 7} \cr & \Rightarrow {S_{ABC}} = {3 \over 7}{S_{ABC}} = {3 \over 7}.294 = 126(c{m^2}) \cr} \)
Vậy \({S_{ADC}} = {S_{ABC}} - {S_{ABD}} = 294 - 126 = 168(c{m^2})\).
-- Mod Toán 8 HỌC247
-


Tính độ dài đoạn MN biết tam giác ABC cân tại B, phân giác của góc A cắt BC tại M
bởi Lan Ha
 31/05/2019
31/05/2019
Bài 1: Cho tam giác ABC cân tại B, phân giác của góc A cắt BC tại M, phân giác của góc C cắt BA tại N. Cho AB=10 cm, AC= 6 cm. Tính độ dài đoạn MN.
Theo dõi (0) 1 Trả lời -


Tính các góc của hình hình thang cân
bởi Lê Tường Vy
 31/07/2019
31/07/2019
Cho Hình thang cân có 3 cạnh bằng nhau và đáy lớn dài gấp đôi đay nhỏ
a, Tinh các góc của hình thang cân
b, Tính chi vi hình thang cân biêt đường cao của chúng bằng 4 căn 3 cm
Theo dõi (0) 1 Trả lời -


Chứng minh 1/DE=1/a+1/b
bởi Nguyễn Anh Hưng
 31/05/2019
31/05/2019
Bài 2: Cho tam giác ABC cân tại A, BC=a, AC=b. Kẻ phân giác BD,CE.Tính DE, từ đó suy ra \(\dfrac{1}{DE}=\dfrac{1}{a}+\dfrac{1}{b}\)
Theo dõi (0) 1 Trả lời -


1.Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng mn.
2.Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC
3.Tam giác ABC có AB= 5cm, AC= 6cm, BC= 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.Theo dõi (0) 1 Trả lời -


Bài 1: Cho \(\bigtriangleup{ABC}\) , AD là đg p/g . Biết AB=15; AC=20 ; BC=25
a) Tính BD; CD
b) Tính tỉ số của S\(\bigtriangleup{ABD}\) : S\(\bigtriangleup{ACB}\)
Bài 2 : Cho \(\bigtriangleup{ABC}\) có: AD, BE, CF là 3 đg p/g
CMR: \(\dfrac{DB}{DC}\) . \(\dfrac{EC}{EA}\). \(\dfrac{FA}{FB}\)= 1
Theo dõi (0) 1 Trả lời






