Giải bài 21 tr 68 sách GK Toán 8 Tập 2
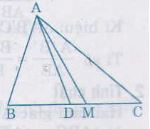
a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM, biết AB= m, AC= n( n>m). Và diện tích của tam giác ABC là S.
b) Cho n = 7cm, m = 3cm. Hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC.
Hướng dẫn giải chi tiết
a) Ta có \(AD\) là đường phân giác của \(∆ABC\) (gt) nên
\(\dfrac{{B{\rm{D}}}}{{DC}} = \dfrac{{AB}}{{AC}}\) (Tính chất đường phân giác của tam giác)
\(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}\) (do hai tam giác có chung chiều cao từ đỉnh A)
Nên \(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}= \dfrac{AB}{AC}= \dfrac{m}{n}\)
\(\eqalign{
& \Rightarrow {{{S_{ADC}}} \over {{S_{ABD}}}} = {n \over m} \cr
& \Rightarrow {{{S_{ADC}}} \over {{S_{ABD}}}} + 1 = {n \over m} + 1 \cr
& \Rightarrow {{{S_{ADC}} + {S_{ABD}}} \over {{S_{ABD}}}} = {{n + m} \over m} \cr} \)
\(\Rightarrow \dfrac{S_{ABD}}{S_{ADC}+S_{ABD}}= \dfrac{m}{n+m}\)
hay \(\dfrac{S_{ABD}}{S_{ABC}}= \dfrac{m}{n+m}\)
\(\Rightarrow {S_{AB{\rm{D}}}} = \dfrac{{mS}}{{n + m}}\)
Vì \(AM\) là trung tuyến của \(∆ABC\) (gt) \(\Rightarrow S_{ABM}= \dfrac{1}{2}S_{ABC}\).
Có \(AB < AC (m<n)\) và AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.
\(\Rightarrow S_{ADM}= S_{ABM}- S_{ABD}\)
\( \Rightarrow S_{ADM} = \dfrac{1}{2}S -\dfrac{m}{n+m}S \)\(\,= \dfrac{S(m+n-2m)}{2(m+n)}\)
\(S_{ADM}= \dfrac{S(n -m)}{2(m+n)}\) (với \(n>m\))
b) Khi \(n = 7cm, m = 3cm\) ta có:
\({S_{A{\rm{D}}M}} = \dfrac{{7 - 3}}{{2\left( {7 + 3} \right)}}.S = \dfrac{S}{5} = \dfrac{{20.S }}{100} \)\(\,= 20\% S\)
Vậy \(S_{ADM} = 20\%S_{ABC}\).
-- Mod Toán 8 HỌC247
-


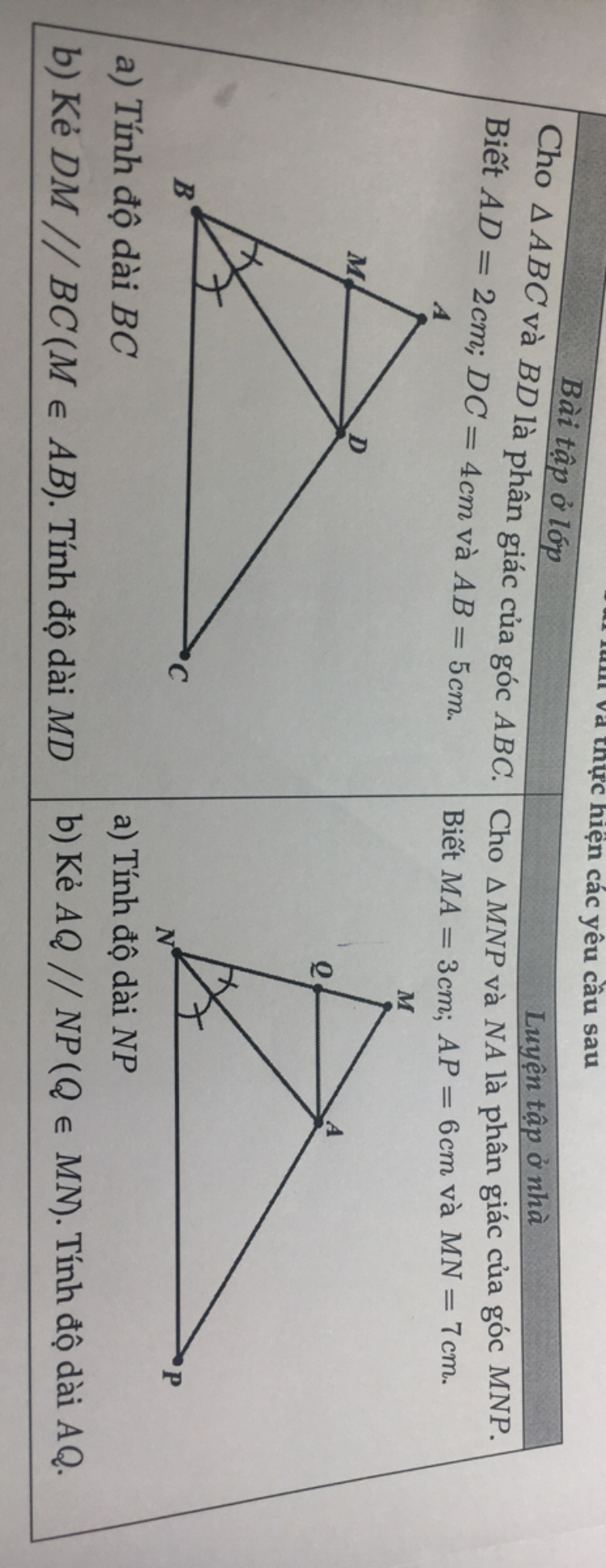
Cho tam giác ABC, BD là tia phân giác góc B, biết AD=2cm, DC=4cm và AB=5cm. Tính độ dào BC
bởi rosie.
 01/03/2020
01/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC, phân giác góc BAC cắt cạnh BC ở D, biết BD=7,5cm, CD=5cm. Qua D kẻ đường thẳng song song với AB cắt AC tại E và AC=10cm. Tính AE, EC, DE.
bởi Mộng Tiêu
 26/02/2020
26/02/2020
Cho tam giác abc,p/g bac cắt cạnh bc ở d,biết bd=7,5cm,cd=5cm.Qua d kẻ đường thẳng song song với ab cắt ac tại e.Tính ae,ec,de nếu ac=10cm
Theo dõi (0) 0 Trả lời -


Cho hình bình hành ABCD, một đường thẳng đi qua A cắt BD, CD, BC tại I, M, N. Phân giác góc ACB cắt BD và AB tại P và E . CMR: PC/PE -AC/BC=1.
bởi Đỗ Khắc Gia Huy
 21/02/2020
21/02/2020
cho hbh ABCD , một đường thẳng đi qua A cắt BD, CD,BC tại I,M,N .Phân giác góc ACB cắt BD và AB tại P và E . CMR : PC/PE -AC/BC=1
Theo dõi (1) 0 Trả lời -


Cho tam giác ABC vuông tại A , đường phân giác của góc BAC cắt cạnh BC ở D . Biết BD = 7,5cm ; CD = 20cm . Tính AB,AC
bởi Huyền Trang
 20/02/2020
Giải bài tập giúp mìnhTheo dõi (0) 0 Trả lời
20/02/2020
Giải bài tập giúp mìnhTheo dõi (0) 0 Trả lời -


 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời
Bài tập SGK khác
Bài tập 19 trang 68 SGK Toán 8 Tập 2
Bài tập 20 trang 68 SGK Toán 8 Tập 2
Bài tập 22 trang 68 SGK Toán 8 Tập 2
Bài tập 17 trang 87 SBT Toán 8 Tập 2
Bài tập 18 trang 87 SBT Toán 8 Tập 2
Bài tập 19 trang 87 SBT Toán 8 Tập 2
Bài tập 20 trang 87 SBT Toán 8 Tập 2
Bài tập 21 trang 88 SBT Toán 8 Tập 2
Bài tập 22 trang 88 SBT Toán 8 Tập 2
Bài tập 23 trang 88 SBT Toán 8 Tập 2
Bài tập 24 trang 88 SBT Toán 8 Tập 2