Giải bài 20 tr 68 sách GK Toán 8 Tập 2
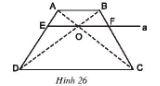
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhat tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC théo thứ tự E và F(h26)
Chứng minh rằng OE = OF.
Hướng dẫn giải chi tiết
\(∆ADC\) có \(OE // DC\) (gt) nên \(\dfrac{OE}{DC} = \dfrac{AO}{AC}\) (1) (hệ quả của định lí TaLet trong tam giác)
\(∆BDC\) có \(OF // DC\) (gt) nên \(\dfrac{OF}{DC} = \dfrac{BF}{BC}\) (2) (hệ quả của định lí TaLet trong tam giác)
\(∆BAC\) có \(OF // AB\) (gt) nên \(\dfrac{AO}{AC} = \dfrac{BF}{BC}\) (3) (hệ quả của định lí TaLet trong tam giác)
Từ (1), (2), (3) suy ra \(\dfrac{OE}{DC} = \dfrac{OF}{DC}\) nên \(OE = OF\).
-- Mod Toán 8 HỌC247
-


Cho hình bình hành ABCD, kẻ các tia phân giác của góc A và D. Các tia phân giác này cắt đường chéo BD và AC lần lượt tại M và N. Chứng minh MN//BC.
bởi Nghiêm Bảo Ngân
 25/03/2020
25/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A , BC=8cm phân giác của góc B cắt đường cao AH ở K , AK/AH=3/5.a) Tính độ dài ABb) Đường thẳng vuông góc với BK cắt AH ở E . Tính EH
bởi Cảnh Nguyễn Trung Cảnh
 19/03/2020
Cho tam giác ABC cân tại A , BC=8cm phân giác của góc B cắt đường cao AH ở K , AK/AH=3/5.a) Tính độ dài ABb) Đường thẳng vuông góc với BK cắt AH ở E . Tính EHTheo dõi (0) 0 Trả lời
19/03/2020
Cho tam giác ABC cân tại A , BC=8cm phân giác của góc B cắt đường cao AH ở K , AK/AH=3/5.a) Tính độ dài ABb) Đường thẳng vuông góc với BK cắt AH ở E . Tính EHTheo dõi (0) 0 Trả lời -


Tỉ số của hai đoạn thẳng EB và EC ?
bởi Trịnh Phương Linh
 16/03/2020
Cho tam giác vuông ABC ,góc A bằng 90°, AB =12 cm ,BC = 20 cm. Kẻ tia phân giác AE của góc BAC. a ,Tính tỉ số của hai đoạn thẳng EB và EC ?b,Tính độ dài các đoạn thẳng AC,BE, EC? c,Kẻ EI vuông góc AC, tính AI,IC( làm tròn đến chữ số thập phân thứ hai)Theo dõi (1) 0 Trả lời
16/03/2020
Cho tam giác vuông ABC ,góc A bằng 90°, AB =12 cm ,BC = 20 cm. Kẻ tia phân giác AE của góc BAC. a ,Tính tỉ số của hai đoạn thẳng EB và EC ?b,Tính độ dài các đoạn thẳng AC,BE, EC? c,Kẻ EI vuông góc AC, tính AI,IC( làm tròn đến chữ số thập phân thứ hai)Theo dõi (1) 0 Trả lời -


Cho ∆ ABC có AD là tia phân giác của ABC. a) Tính DC biết BC=4cm;AB=12cm;AC=15cm b) Biết DE//AB. Tính DE
bởi Tùng
 13/03/2020
Mình cần gấp plsTheo dõi (2) 4 Trả lời
13/03/2020
Mình cần gấp plsTheo dõi (2) 4 Trả lời -


Cho hình tứ giác ABCD ve AE vuông góc BD tại E, CF vuông góc BD tại F a, chứng minh AECF là hình thang cân b, gọi M là giao điểm của AE và CD,Ngay giao điểm của CF và AB, O là trung điểm của AC. Chứng minh M, O, N thẳng hàng
bởi Như Quỳnh
 04/03/2020
Mọi người giúp em bài 2 với ạ
04/03/2020
Mọi người giúp em bài 2 với ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 18 trang 68 SGK Toán 8 Tập 2
Bài tập 19 trang 68 SGK Toán 8 Tập 2
Bài tập 21 trang 68 SGK Toán 8 Tập 2
Bài tập 22 trang 68 SGK Toán 8 Tập 2
Bài tập 17 trang 87 SBT Toán 8 Tập 2
Bài tập 18 trang 87 SBT Toán 8 Tập 2
Bài tập 19 trang 87 SBT Toán 8 Tập 2
Bài tập 20 trang 87 SBT Toán 8 Tập 2
Bài tập 21 trang 88 SBT Toán 8 Tập 2
Bài tập 22 trang 88 SBT Toán 8 Tập 2
Bài tập 23 trang 88 SBT Toán 8 Tập 2
Bài tập 24 trang 88 SBT Toán 8 Tập 2