Với bài học này chúng ta sẽ cùng tìm hiểu về Khi nào góc xOy + góc yOz= góc xOz?, cùng với các ví dụ minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng ghi nhớ kiến thức
Tóm tắt lý thuyết
1.1. Khi nào thì tổng số đo hai góc xOy và yOz bằng số đo góc xOz?
Nếu tia Oy nằm giữa hai tia Ox và Oz thì \(\widehat {xOy}\,\, + \,\widehat {yOz\,}\, = \,\widehat {xOz}\)
Ngược lại, nếu \(\widehat {xOy}\,\, + \,\widehat {yOz\,}\, = \,\widehat {xOz}\)thì tia Oy nằm giữa hai tia Ox, Oz.
1.2. Hai góc kề nhau, phụ nhau, bù nhau, kề bù
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh nhau. Chẳng hạn trên hình, \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề nhau, cạnh chung là Oy.
.png)
Hai góc phụ nhau là hai góc có tổng số đo bẳng \({90^0}\), chẳng hạn góc \({50^0}\) và góc \({40^0}\) là hai góc phụ nhau.
Hai góc bù nhau là hai góc có tổng số đo bẳng \({180^0}\), chẳng hạn góc \({110^0}\) và góc \({70^0}\) là hai góc bù nhau.
Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.
Ví dụ 1: Gọi Oz là tia nằm giữa hai tia Ox, Oy. Biết \(\widehat {xOy}\, = \,{a^0},\,\widehat {zOx}\, = \,{b^0}.\) Tính \(\widehat {yOz}\)?
Giải
\(\widehat {yOz} = \widehat {xOy} - \widehat {zOx}\, = \,{a^0}\, - \,{b^0}.\)
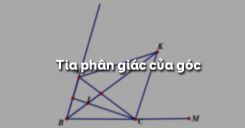
Ví dụ 2: Ở hình, hai tia OI, OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết \(\widehat {KOA}\, = \,\,{120^0},\,\widehat {BOI}\, = \,{45^0}.\) Tính \(\widehat {KOB},\,\widehat {AOI},\,\widehat {BOA}.\)
.png)
Giải
\(\begin{array}{l}\widehat {KOB}\, = {180^0}\, - \,{45^0}\, = \,{135^0}\\\widehat {AOI}\,\, = \,{180^0}\, - \,{120^0}\, = \,{60^0}\\\,\widehat {BOA}\, = {45^0}\, + {60^0}\, = \,{105^0}\end{array}\)
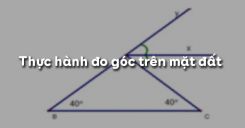
Ví dụ 3: Xem hình, làm thế nào để chỉ đo hai góc mà biết được số đo của cả ba góc xOy, xOz, yOz?
.png)
Giải
Có ba cách đo, chẳng hạn đo \(\widehat {xOy},\,\widehat {yOz}\) suy ra \(\widehat {xOz}\)
Bài tập minh họa
Bài 1: Tia Oy nằm giữa hai tia Ox và Oz. Biết \(\widehat {xOy} = {40^0}\). Hỏi góc xOz là nhọn, vuông, tù hay bẹt nếu số đo của góc yOz lần lượt là \({30^0},{50^0},{70^0},{140^0}\)?
Giải
\(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
\({40^0} + {30^0} = {70^0}\) Vậy \(\widehat {xOz}\) là góc nhọn.
\({40^0} + {50^0} = {90^0}\) Vậy \(\widehat {xOz}\) là góc vuông.
Bài 2: Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm O nằm ngoài đường thẳng d. Biết \(\widehat {AOD} = {30^0},\,\widehat {DOC} = {40^0},\,\widehat {AOB}\, = \,{90^0}.\) Tính \(\widehat {AOC},\,\widehat {COB}.\)
Giải
\(\begin{array}{l}\widehat {AOC} = \,{30^0} + {40^0} = {70^0}\\\,\widehat {COB} = {90^0} - {70^0} = {20^0}\end{array}\)
Bài 3: Cho hình
.png)
a. Gọi tên các cặp góc kề nhau đỉnh O trong hình đó.
b. Cho biết số đo của các góc đỉnh O trong hình đó.
c. Cho biết những cặp góc phụ nhau đỉnh O
d. Cho biết những cặp góc bù nhau đỉnh O.
e. Cho biết những cặp góc kề bù nhau đỉnh O.
Giải
a. Các cặp góc kề nhau đỉnh O là: mOn và nOw; mOn và nOz; mOn và nOt; mOw và zOw; mOw và tOw; mOz và zOt; wOn và zOw; wOn và tOw; wOz và zOt.
b. \(\widehat {mOt} = {180^0};\,\widehat {mO{\rm{w}}}\, = {90^0};\,\widehat {nO{\rm{w}}}\, = {60^0};\,\widehat {{\rm{w}}Oz} = {45^0}\)
c. mOn và nOw; wOz và zOt
d. mOn và nOt; wOm và wOt; mOz và zOt
e. mOn và nOt; wOm và wOt; mOz và zOt.
3. Luyện tập Bài 4 Chương 2 Hình học 6
Qua bài giảng Khi nào góc xOy + góc yOz= góc xOz? này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Khi nào thì tổng số đo hai góc xOy và yOz bằng số đo góc xOz
- Phân biệt hai góc kề nhau, phụ nhau, bù nhau, kề bù
3.1 Trắc nghiệm về Khi nào góc xOy + góc yOz= góc xOz? - Hình học 6
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 6 Bài 4 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. Hai góc tù là hai góc kề nhau
- B. Cho 3 tia chung gốc Ox, Oy, Oz ta luôn có:\(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
- C. Nếu tia Oy nằm giữa hai tia On và Om thì khi đó ta có \(\widehat {yOn} + \widehat {yOm} = \widehat {mOn}\)
- D. Nếu góc A và góc B là hai góc bù nhau thì \(\widehat A + \widehat B = {90^0}\)
-
- A. Tia Ox nằm giữa hai tia Oy và Oz
- B. Tia Oy nằm giữa hai tia Oz và Ox
- C. Tia Oz nằm giữa hai tia Oy và Ox
- D. Chưa thể kết luận được tia nào nằm giữa hai tia còn lại
-
Câu 3:
Cho góc xOy và góc yOy' là hai góc kề bù. Biết \(\widehat {xOy} = {80^0}\), số đo của góc yOy' là:
- A. 1000
- B. 700
- C. 800
- D. 600
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2 Bài tập SGK về Khi nào góc xOy + góc yOz= góc xOz? - Hình học 6
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 6 Bài 4 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 6 tập 2
Bài tập 16 trang 86 SBT Toán 6 Tập 2
Bài tập 17 trang 86 SBT Toán 6 Tập 2
Bài tập 20 trang 87 SBT Toán 6 Tập 2
Bài tập 21 trang 87 SBT Toán 6 Tập 2
Bài tập 22 trang 87 SBT Toán 6 Tập 2
Bài tập 18 trang 86 SBT Toán 6 Tập 2
Bài tập 23 trang 87 SBT Toán 6 Tập 2
Bài tập 4.1 trang 87 SBT Toán 6 Tập 2
Bài tập 19 trang 87 SBT Toán 6 Tập 2
Bài tập 4.2 trang 88SBT Toán 6 Tập 2
Bài tập 4.3 trang 87 SBT Toán 6 Tập 2
Bài tập 18 trang 82 SGK Toán 6 Tập 2
Bài tập 19 trang 82 SGK Toán 6 Tập 2
Bài tập 20 trang 82 SGK Toán 6 Tập 2
Bài tập 21 trang 82 SGK Toán 6 Tập 2
Bài tập 22 trang 82 SGK Toán 6 Tập 2
Bài tập 23 trang 83 SGK Toán 6 Tập 2
4. Hỏi đáp Bài 4 Chương 2 Hình học 6
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 6 HỌC247