Luyện tập 2 trang 106 SGK Toán 11 Cánh diều Tập 1 - CD

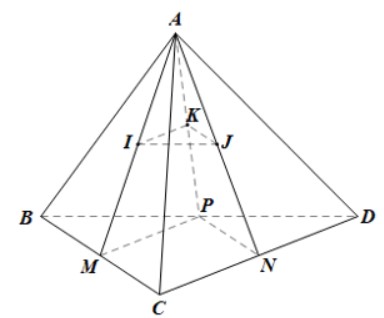
Trong mặt phẳng \((AMP)\), xét $∆\backslash ($AMP\) có I, K lần lượt là trung điểm của AM, AP nên IK là đường trung bình

Do đó \(IK // MP\).

Mà \(MP ⊂ (BCD)\) nên \(IK // (BCD)\).

Trong mặt phẳng \((ANP)\), xét $∆\backslash ($ANP\) có J, K lần lượt là trung điểm của AN, AP nên JK là đường trung bình

Do đó \(JK // NP\).

Mà \(NP ⊂ (BCD)\) nên \(JK // (BCD)\).

Ta có: \(IK // (BCD)\);

\(JK // (BCD)\);

IK, JK cắt nhau tại điểm K và cùng nằm trong mặt phẳng \((IJK)\).

Suy ra \((IJK) // (BCD)\).

-- Mod Toán 11 HỌC247