Luyện tập 3 trang 108 SGK Toán 11 Cánh diều Tập 1
Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự tại A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A’, B’. Chứng minh rằng AB = A’B’?
Hướng dẫn giải chi tiết Luyện tập 3
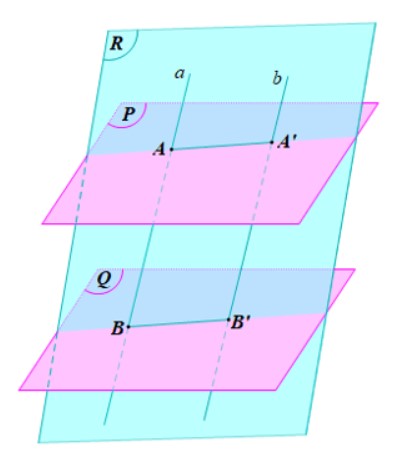
Giả sử \((R) = (a, b)\).
Ta có: \(A ∈ (R)\) và \(A ∈ (P)\) nên A là giao điểm của hai mặt phẳng (R) và (P).
\(A’ ∈ (R)\) và \(A’ ∈ (P)\) nên A’ là giao điểm của hai mặt phẳng (R) và (P).
Do đó \((R) ∩ (P) = AA’\).
Tương tự ta cũng có \((R) ∩ (Q) = BB’\).
Do \((P) // (Q)\);
\((R) ∩ (P) = AA’\);
\((R) ∩ (Q) = BB’\)
Suy ra \(AA’ // BB’\)
Trong mp(R), xét tứ giác \(ABB’A’\) có: \(AA’ // BB’\) và \(AB // A’B’\) (do \(a // b\))
Suy ra \(ABB’A’\) là hình bình hành
Do đó \(AB = A’B’\).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 3 trang 106 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 4 trang 107 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 5 trang 108 SGK Toán 11 Cánh diều Tập 1 - CD
Luyện tập 4 trang 109 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 1 trang 109 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 2 trang 109 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 3 trang 109 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 4 trang 109 SGK Toán 11 Cánh diều Tập 1 - CD
Bài tập 28 trang 108 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 29 trang 108 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 30 trang 108 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 31 trang 108 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 32 trang 108 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 33 trang 108 SBT Toán 11 Tập 1 Cánh diều - CD





