Bài tập 31 trang 108 SBT Toán 11 Tập 1 Cánh diều
Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng phân biệt. Khẳng định nào sau đây là đúng?
A. \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)
B. \(AD\parallel \left( {BEF} \right)\)
C. \(\left( {ABC} \right)\parallel \left( {DEF} \right)\)
D. \(EC\parallel \left( {ABD} \right)\)
Hướng dẫn giải chi tiết Bài tập 31
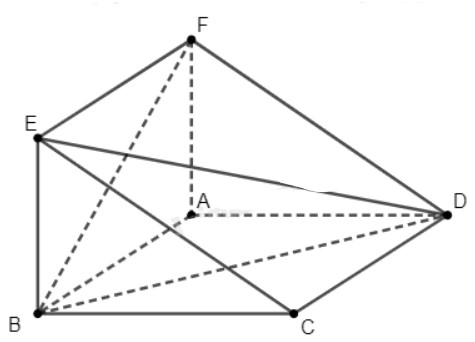
Do \(ABCD\) là hình bình hành nên \(AD\parallel BC\). Mà \(BC \subset \left( {BCE} \right)\), ta suy ra \(AD\parallel \left( {BCE} \right)\).
Chứng minh tương tự ta có \(AF\parallel \left( {BCE} \right)\).
Như vậy \(\left( {ADF} \right)\parallel \left( {BCE} \right)\).
Ta có \(A \in AD\), \(A \in \left( {BEF} \right)\) nên suy ra \(AD\) và \(\left( {BEF} \right)\) có điểm chung, tức là chúng không song song với nhau.
Tương tự, ta cũng chứng minh được \(EC\) và \(\left( {ABD} \right)\) không song song với nhau.
Do \(AB\parallel CD\), \(AB\parallel EF\) nên \(CD\parallel EF\), tức là tứ giác \(CDFE\) là hình bình hành.
Vì \(C \in \left( {ABC} \right)\), \(C \in \left( {DEF} \right)\), nên hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {DEF} \right)\) có điểm chung, tức là chúng không song song với nhau.
Đáp án đúng là A.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





