Bài 3 trang 109 SGK Toán 11 Cánh diều Tập 1 - CD

a)

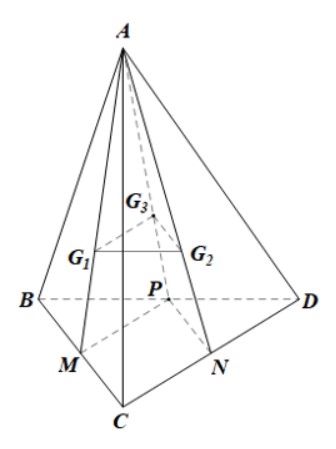
Gọi M, N, P lần lượt là trung điểm của BC, CD, DB.

Trong mp(ABC), xét $∆$ABC có G₁ là trọng tâm của tam giác nên $\frac{A{G}_1}{AM}=\frac{2}{3}$ ;

Trong mp(ACD), xét $∆$ACD có G₂ là trọng tâm của tam giác nên $\frac{A{G}_2}{AN}=\frac{2}{3}$ ;

Trong mp(ABD), xét $∆$ABD có G₃ là trọng tâm của tam giác nên $\frac{A{G}_3}{AP}=\frac{2}{3}$ .

Trong mp(AMP), xét $∆$AMP có $\frac{A{G}_1}{AM}=\frac{A{G}_3}{AP}=\frac{2}{3}$ nên G₁G₃­ // MP (theo định lí Thalès đảo).

Mà MP ⊂ (BCD) nên G₁G₃­ // (BCD).

Chứng minh tương tự ta cũng có $\frac{A{G}_2}{AN}=\frac{A{G}_3}{AP}=\frac{2}{3}$ nên G₂G₃ // NP (theo định lí Thalès đảo).

Mà NP ⊂ (BCD) nên G₂G₃­ // (BCD).

Ta có: G₁G₃­ // (BCD);

G₂G₃­ // (BCD);

G₁G₃, G₂G₃ cắt nhau tại G₃ và cùng nằm trong mp(G₁G₂G₃).

Do đó (G₁G₂G₃) // (BCD).

b)

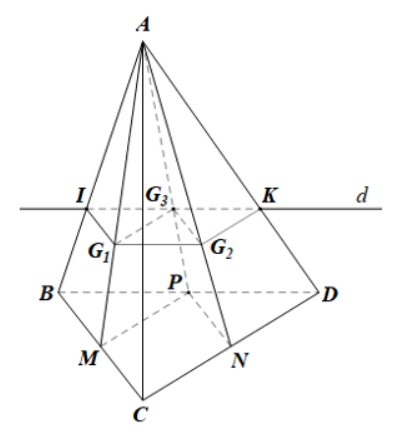
Ta có: B, D cùng thuộc hai mặt phẳng (ABD) và (BCD) nên (ABD) ∩ (BCD) = BD.

Giả sử (ABD) ∩ (G₁G₂G₃) = d.

Ta có: (G₁G₂G₃) // (BCD);

(ABD) ∩ (BCD) = BD;

(ABD) ∩ (G₁G₂G₃) = d.

Suy ra d // BD.

Mà G₃ ∈ (ABD) và G₃ ∈ (G₁G₂G₃) nên G_3­ là giao điểm của (G₁G₂G₃) và (ABD).

Do đó giao tuyến d của hai mặt phẳng (G₁G₂G₃) và (ABD) đi qua điểm G₃ và song song với BD, cắt AB, AD lần lượt tại I và K.

Vậy (G₁G₂G₃) ∩ (ABD) = IK.

-- Mod Toán 11 HỌC247