Hoạt động 6 trang 14 SGK Toán 11 Kết nối tri thức tập 1
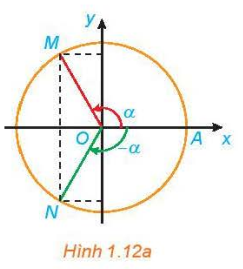
Xét hai điểm M, N trên đường tròn lượng giác xác định bởi hai góc đối nhau (H1.12a).
a) Có nhận xét gì về vị trí của hai điểm M, N đối với hệ trục Oxy. Từ đó rút ra liên hệ giữa cos(−α) và cosα; sin(−α) và sinα.
b) Từ kết quả HĐ6a, rút ra liên hệ giữa: tan(−α) và tanα; cot(−α) và cotα.
Hướng dẫn giải chi tiết Hoạt động 6
Phương pháp giải:
Dựa vào hình vẽ để nhận xét
Lời giải chi tiết:
a) Giả sử M(xM; yM), N(xN; yN).
Từ Hình 1.12a, ta thấy hai điểm M và N đối xứng với nhau qua trục hoành Ox, do đó ta có: xM = xN và yM = – yN.
Theo định nghĩa giá trị lượng giác của một góc, ta lại có:
cos α = xM và cos (– α) = xN. Suy ra cos (– α) = cos α.
sin α = yM và sin (– α) = yN. Suy ra sin α = – sin (– α) hay sin (– α) = – sin α.
b) Ta có:
;
.
Vậy tan (– α) = – tan α; cot (– α) = – cot α.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 5 trang 13 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 6 trang 14 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 7 trang 15 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Vận dụng 2 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.1 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.2 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.3 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.4 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.5 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.6 trang 16 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Bài tập 1.1 trang 7 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.2 trang 7 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.3 trang 7 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.4 trang 7 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.5 trang 7 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.6 trang 7 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.7 trang 8 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.8 trang 8 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.9 trang 8 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT