HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 6 B├Āi 2 Ph├®p t├Łnh l├┤garit m├┤n To├Īn lß╗øp 11 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 14 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
─Éß╗Ö lß╗øn \(M\) (theo ─æß╗Ö Richter) cß╗¦a mß╗Öt trß║Łn ─æß╗Öng ─æß║źt ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh nhŲ░ Hoß║Īt ─æß╗Öng mß╗¤ ─æß║¦u.
a) T├¼m ─æß╗Ö lß╗øn theo thang Richter cß╗¦a c├Īc trß║Łn ─æß╗Öng ─æß║źt c├│ bi├¬n ─æß╗Ö lß╗øn nhß║źt lß║¦n lŲ░ß╗Żt l├Ā \({10^{3,5}}\mu m;100000\mu m;{100.10^{4,3}}\mu m\).
b) Mß╗Öt trß║Łn ─æß╗Öng ─æß║źt c├│ bi├¬n ─æß╗Ö lß╗øn nhß║źt \(A = 65000\mu m\) th├¼ ─æß╗Ö lß╗øn \(M\) cß╗¦a n├│ phß║Żi thoß║Ż m├Żn hß╗ć thß╗®c n├Āo?
-
Thß╗▒c h├Ānh 1 trang 15 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├Łnh:
a) \({\log _3}\sqrt[3]{3}\);
b) \({\log _{\frac{1}{2}}}8\);
c) \({\left( {\frac{1}{{25}}} \right)^{{{\log }_5}4}}\).
-
Thß╗▒c h├Ānh 2 trang 16 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Sß╗Ł dß╗źng m├Īy t├Łnh cß║¦m tay, t├Łnh gi├Ī trß╗ŗ c├Īc biß╗āu thß╗®c sau (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® s├Īu):
a) \({\log _5}0,5\);
b) \(\log 25\);
c) \(\ln \frac{3}{2}\).
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 2 trang 16 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Cho c├Īc sß╗æ thß╗▒c dŲ░ŲĪng \(a,M,N\) vß╗øi \(a \ne 1\). Bß║Īn Qu├ón ─æ├Ż vß║Į sŲĪ ─æß╗ō v├Ā t├¼m ra c├┤ng thß╗®c biß║┐n ─æß╗Ģi biß╗āu thß╗®c \({\log _a}\left( {MN} \right)\) nhŲ░ sau:
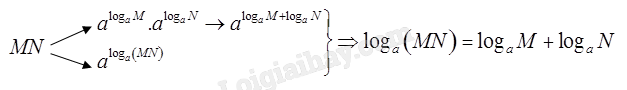
a) Giß║Żi th├Łch c├Īch l├Ām cß╗¦a bß║Īn Qu├ón.
b) Vß║Į sŲĪ ─æß╗ō tŲ░ŲĪng tß╗▒ ─æß╗ā t├¼m c├┤ng thß╗®c biß║┐n ─æß╗Ģi cho \({\log _a}\frac{M}{N}\) v├Ā \({\log _a}{M^\alpha }\left( {\alpha \in \mathbb{R}} \right)\).
-
Thß╗▒c h├Ānh 3 trang 17 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├Łnh:
a) \({\log _5}4 + {\log _5}\frac{1}{4}\);
b) \({\log _2}28 - {\log _2}7\); c) \(\log \sqrt {1000} \).
-
Vß║Łn dß╗źng trang 17 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
─Éß╗Ö lß╗øn \(M\) cß╗¦a mß╗Öt trß║Łn ─æß╗Öng ─æß║źt theo thang Richter ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c \(M = \log \frac{A}{{{A_0}}}\), trong ─æ├│ \(A\) l├Ā bi├¬n ─æß╗Ö lß╗øn nhß║źt ghi ─æŲ░ß╗Żc bß╗¤i m├Īy ─æo ─æß╗ŗa chß║źn, \({A_0}\) l├Ā bi├¬n ─æß╗Ö ti├¬u chuß║®n ─æŲ░ß╗Żc sß╗Ł dß╗źng ─æß╗ā hiß╗ću chß╗ēnh ─æß╗Ö lß╗ćch g├óy ra bß╗¤i khoß║Żng c├Īch cß╗¦a m├Īy ─æo ─æß╗ŗa chß║źn so vß╗øi t├óm chß║źn (ß╗¤ Hoß║Īt ─æß╗Öng mß╗¤ ─æß║¦u v├Ā Hoß║Īt ─æß╗Öng 1, \({A_0} = 1\mu m\)).
a) T├Łnh ─æß╗Ö lß╗øn cß╗¦a trß║Łn ─æß╗Öng ─æß║źt c├│ bi├¬n ─æß╗Ö \(A\) bß║▒ng
i) \({10^{5,1}}{A_0}\); ii) \(65000{A_0}\).
b) Mß╗Öt trß║Łn ─æß╗Öng ─æß║źt tß║Īi ─æß╗ŗa ─æiß╗ām \(N\) c├│ bi├¬n ─æß╗Ö lß╗øn nhß║źt gß║źp ba lß║¦n bi├¬n ─æß╗Ö lß╗øn nhß║źt cß╗¦a trß║Łn ─æß╗Öng ─æß║źt tß║Īi ─æß╗ŗa ─æiß╗ām \(P\). So s├Īnh ─æß╗Ö lß╗øn cß╗¦a hai trß║Łn ─æß╗Öng ─æß║źt.
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 3 trang 18 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Khi chŲ░a c├│ m├Īy t├Łnh, ngŲ░ß╗Øi ta thŲ░ß╗Øng t├Łnh c├Īc l├┤garit dß╗▒a tr├¬n bß║Żng gi├Ī trß╗ŗ c├Īc l├┤garit thß║Łp ph├ón ─æ├Ż ─æŲ░ß╗Żc x├óy dß╗▒ng sß║Ąn. Chß║│ng hß║Īn, ─æß╗ā t├Łnh \(x = {\log _2}15\), ngŲ░ß╗Øi ta viß║┐t \({2^x} = 15\) rß╗ōi lß║źy l├┤garit thß║Łp ph├ón hai vß║┐, nhß║Łn ─æŲ░ß╗Żc \(x\log 2 = \log 15\) hay \(x = \frac{{\log 15}}{{\log 2}}\).
Sß╗Ł dß╗źng c├Īch l├Ām n├Āy, t├Łnh \({\log _a}N\) theo \(\log a\) v├Ā \(\log N\) vß╗øi \(a,N > 0,a \ne 1\).
-
Thß╗▒c h├Ānh 4 trang 18 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├Łnh gi├Ī trß╗ŗ c├Īc biß╗āu thß╗®c sau:
a) \({\log _{\frac{1}{4}}}8\);
b) \({\log _4}5.{\log _5}6.{\log _6}8\).
-
Thß╗▒c h├Ānh 5 trang 18 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
─Éß║Ęt \({\log _3}2 = a,{\log _3}7 = b\). Biß╗āu thß╗ŗ \({\log _{12}}21\) theo \(a\) v├Ā \(b\).
-
Giß║Żi B├Āi 1 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├Łnh gi├Ī trß╗ŗ c├Īc biß╗āu thß╗®c sau:
a) \({\log _2}16\);
b) \({\log _3}\frac{1}{{27}}\);
c) \(\log 1000\);
d) \({9^{{{\log }_3}12}}\).
-
Giß║Żi B├Āi 2 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├¼m c├Īc gi├Ī trß╗ŗ cß╗¦a \(x\) ─æß╗ā biß╗āu thß╗®c sau c├│ ngh─®a:
a) \({\log _3}\left( {1 - 2{\rm{x}}} \right)\);
b) \({\log _{x + 1}}5\).
-
Giß║Żi B├Āi 3 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Sß╗Ł dß╗źng m├Īy t├Łnh cß║¦m tay, t├Łnh gi├Ī trß╗ŗ c├Īc biß╗āu thß╗®c sau (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® tŲ░):
a) \({\log _3}15\);
b) \(\log 8 - \log 3\);
c) \(3\ln 2\).
-
Giß║Żi B├Āi 4 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├Łnh gi├Ī trß╗ŗ c├Īc biß╗āu thß╗®c sau:
a) \({\log _6}9 + {\log _6}4\);
b) \({\log _5}2 - {\log _5}50\);
c) \({\log _3}\sqrt 5 - \frac{1}{2}{\log _3}15\).
-
Giß║Żi B├Āi 5 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
T├Łnh gi├Ī trß╗ŗ c├Īc biß╗āu thß╗®c sau:
a) \({\log _2}9.{\log _3}4\);
b) \({\log _{25}}\frac{1}{{\sqrt 5 }}\);
c) \({\log _2}3.{\log _9}\sqrt 5 .{\log _5}4\).
-
Giß║Żi B├Āi 6 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
─Éß║Ęt \(\log 2 = a,\log 3 = b\). Biß╗āu thß╗ŗ c├Īc biß╗āu thß╗®c sau theo \(a\) v├Ā \(b\).
a) \({\log _4}9\);
b) \({\log _6}12\);
c) \({\log _5}6\).
-
Giß║Żi B├Āi 7 trang 19 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
a) NŲ░ß╗øc cß║źt c├│ nß╗ōng ─æß╗Ö H+ l├Ā \({10^{ - 7}}\) mol/L. T├Łnh ─æß╗Ö pH cß╗¦a nŲ░ß╗øc cß║źt.
b) Mß╗Öt dung dß╗ŗch c├│ nß╗ōng ─æß╗Ö H+ gß║źp 20 lß║¦n nß╗ōng ─æß╗Ö H+ cß╗¦a nŲ░ß╗øc cß║źt. T├Łnh ─æß╗Ö pH cß╗¦a dung dß╗ŗch ─æ├│.
-
B├Āi tß║Łp 1 trang 12 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
T├Łnh gi├Ī trß╗ŗ cß╗¦a c├Īc biß╗āu thß╗®c sau:
a) ;
b) log 10 000;
c) log 0,001;
d) log0,7 1;
e) ;
g) log0,5 0,125.
-
B├Āi tß║Łp 2 trang 12 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
T├Łnh gi├Ī trß╗ŗ cß╗¦a c├Īc biß╗āu thß╗®c sau:
a) ;
b) eln 3;
c) ;
d) ;
e) ;
g) 0,001log2.
-
B├Āi tß║Łp 3 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
T├Łnh gi├Ī trß╗ŗ cß╗¦a c├Īc biß╗āu thß╗®c sau:
a) ;
b) log5 75 + log5 3;
c) ;
d) 4log12 2 + 2log12 3;
e) ;
g) .
-
B├Āi tß║Łp 4 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
T├Łnh gi├Ī trß╗ŗ cß╗¦a c├Īc biß╗āu thß╗®c sau:
a) ;
b) log5 3 . log3 5;
c) ;
d) log27 25 . log5 81.
-
B├Āi tß║Łp 5 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
T├Łnh:
a) log3 5. log5 7 .log7 9;
b) .
-
B├Āi tß║Łp 6 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Sß╗Ł dß╗źng m├Īy t├Łnh cß║¦m tay, t├Łnh (l├Ām tr├▓n ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® tŲ░):
a) log7 21;
b) log 2,25;
c) ;
d) log0,5 3 + log5 0,3.
-
B├Āi tß║Łp 7 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
─Éß║Ęt log2 3 = a, log2 5 = b. H├Ży biß╗āu thß╗ŗ c├Īc biß╗āu thß╗®c sau theo a v├Ā b.
a) log┬Ł2 45;
b) ;
c) log3 20.
-
B├Āi tß║Łp 8 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
─Éß║Ęt log x = a, log y = b, log z = c (x, y, z > 0). H├Ży biß╗āu thß╗ŗ c├Īc biß╗āu thß╗®c sau theo a, b, c.
a) log (xyz);
b) ;
c) logz (xy2) z ŌēĀ 1.
-
B├Āi tß║Łp 9 trang 13 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
─Éß║Ęt log2 3 = a, log3 15 = b. Biß╗āu thß╗ŗ log3018 theo a v├Ā b?






