Hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 1 Bài 4 Hàm số lượng giác và đồ thị môn Toán lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 25 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vì sao mặt cắt của sóng nước trên mặt hồ được gọi là có dạng hình sin?

-
Hoạt động khám phá 1 trang 25 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác, hãy giải thích vì sao xác định duy nhất:
a) Giá trị sint và cost;
b) Giá trị tant (nếu ) và cot t (nếu ).
-
Hoạt động khám phá 2 trang 26 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
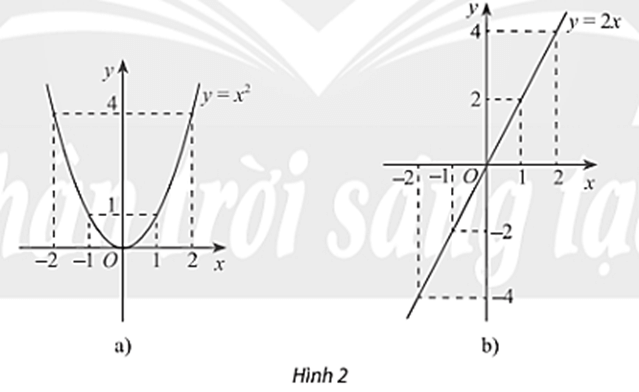
Xét hai hàm số y = x2, y = 2x và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp nêu mối liên hệ của giá trị hàm số tại 1 và – 1, 2 và – 2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
-
Thực hành 1 trang 27 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.
-
Hoạt động khám phá 3 trang 27 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi x ∈ℝ.
-
Thực hành 2 trang 27 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx.
-
Hoạt động khám phá 4 trang 28 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

-
Hoạt động khám phá 5 trang 28 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

-
Thực hành 3 trang 30 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hàm số y = cos x với \(x \in \left [ -\frac{\pi }{2};\pi \right ]\)
a) Vẽ đồ thị hàm số đã cho
b) Tại các điểm nào thì giá trị hàm số lớn nhất?
c) Tìm các giá trị của x thuộc \(\left [ -\frac{\pi }{4};\frac{5\pi }{4} \right ]\) sao cho \(\sin(x-\frac{\pi }{4})<0\)
-
Vận dụng 1 trang 30 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
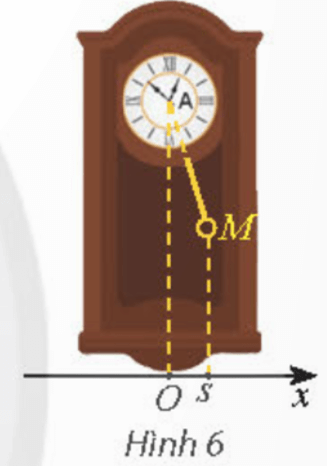
Li độ s(cm) của một con lắc đồng hồ theo thời gian t(giây) được cho bởi hàm số s = 2cosπt. Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 3 giây đầu thì con lắc có li độ lớn nhất.
(Theo https://www.britannica.com/science/simple-harmonic-motion)
-
Hoạt động khám phá 6 trang 30 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.
-
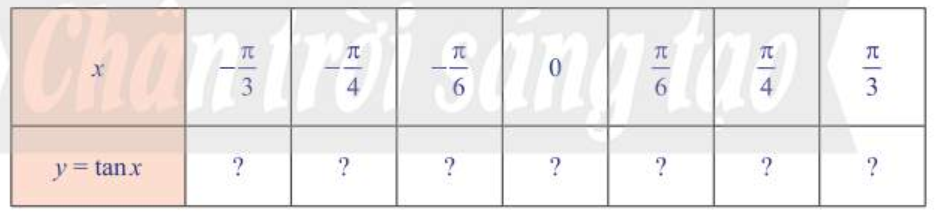
Hoạt động khám phá 7 trang 31 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

-
Thực hành 4 trang 32 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Có bao nhiêu giá trị x trên đoạn [–2π; 2π] thỏa mãn điều kiện tanx = 2?
-
Vận dụng 2 trang 32 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
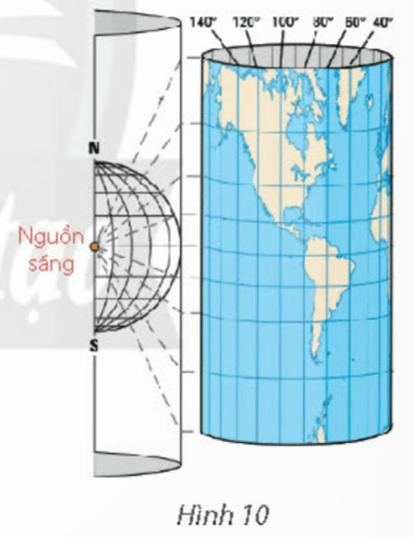
Trong địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoàng và kinh tuyến 00 làm trục tung. Khi đó tung độ của một điểm có vĩ độ φo(-90 < φ< 90) được cho bởi hàm số y = 20tan (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20 cm trên bản đồ.
(Theo https://geologyscience.com/geology/types-of-maps/)
-
Giải Bài 1 trang 32 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Các hàm số dưới đây có là hàm số chẵn hay hàm số lẻ không?
a) y = 5sin2x + 1;
b) y = cosx + sinx;
c) y = tan2x.
-
Giải Bài 2 trang 32 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tìm tập xác định của các hàm số sau:
a) ;
b) ;
c) .
-
Giải Bài 3 trang 33 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tìm tập giá trị của hàm số y = 2cosx + 1.
-
Giải Bài 4 trang 33 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Dựa vào đồ thị hàm số y = sinx, xác định các giá trị x ∈ [– π; π] thỏa mãn sinx = .
-
Giải Bài 5 trang 33 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác α = (Ox, OM) theo hàm số vx = 0,3sin α (m/s) (Hình 11).
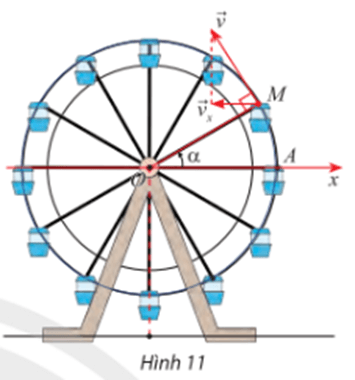
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của vx.
b) Dựa vào độ thị của hàm số sin, hãy cho viết trong các vòng quay đầu tiên (0 ≤ α ≤ 2π), góc α ở trong các khoảng nào thì vx tăng.
-
Giải Bài 6 trang 33 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12).
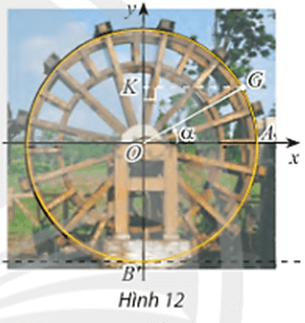
a) Viết hàm số h biểu diễn chiều cao (tính bằng mét) của gàu G so với mặt nước theo góc α = (OA, OG).
b) Guồng nước quay hết mỗi vòng trong 30 giây. Dựa vào đồ thị của hàm số sin hãy cho biết ở các thời điểm t nào trong 1 phút đầu, khoảng cách của gàu đến mặt nước bằng 1,5m.
-
Giải Bài 7 trang 33 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, α là góc lượng giác (Tx, TA) (0 < α < π).
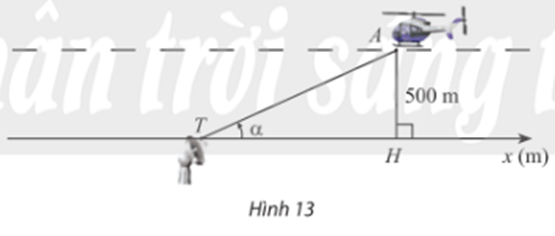
a) Biểu diễn tọa độ xH của điểm H trên trục Tx theo α.
b) Dựa vào đồ thị hàm số côtang, hãy cho biết với thì xH nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.
-
Bài tập 1 trang 26 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tìm tập xác định của các hàm số sau:
a)
b)
c)
d)
-
Bài tập 2 trang 26 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Xét tính chẵn, lẻ của các hàm số sau:
a)
b)
c)
d)
e)
f)
-
Bài tập 3 trang 26 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Tìm tập giá trị của các hàm số sau:
a) y = 5 - ;
b) y = |sin3x| - 1;
c) y = 2tanx + 3;
d) y = + 2.
-
Bài tập 4 trang 27 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hàm số y = sinx với x ∈ [‒2π; 2π].
a) Vẽ đồ thị hàm số đã cho.
b) Tìm các giá trị của sao cho
c) Tìm các giá trị của sao cho
d) Tìm m để có bốn giá trị α ∈ [‒2π; 2π] phân biệt thỏa mãn sinα = m.
-
Bài tập 5 trang 27 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hàm số y = tanx với
a) Vẽ đồ thị hàm số đã cho.
b) Tìm các giá trị của sao cho
c) Tìm các giá trị của sao cho
-
Bài tập 6 trang 27 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi nuôi dưỡng các mô trong cơ thể. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo ra. Giả sử huyết áp của một người thay đổi theo thời gian được cho bởi công thức: p(t) = 120 + 15cos150πt, trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian t tính theo đơn vị phút.
a) Chứng minh p(t) là một hàm số tuần hoàn.
b) Huyết áp cao nhất và huyết áp thấp nhất lần lượt được gọi là huyết áp tâm thu và huyết áp tâm trương. Tìm chỉ số huyết áp của người đó, biết rằng chỉ số huyết áp được viết là huyết áp tâm thu/huyết áp tâm trương.
-
Bài tập 8 trang 27 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Một chất điểm dao động điều hòa theo phương trình với s tính bằng cm và t tình bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì






