HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 6 B├Āi 18 H├Ām sß╗æ bß║Łc hai gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng 1 trang 25 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho phŲ░ŲĪng tr├¼nh \(\sqrt{x^{2}-3x+2}=\sqrt{-x^{2}-2x+2}\)
a) B├¼nh phŲ░ŲĪng hai vß║┐ phŲ░ŲĪng tr├¼nh ─æß╗ā khß╗Ł c─ān v├Ā giß║Żi phŲ░ŲĪng tr├¼nh bß║Łc hai nhß║Łn ─æŲ░ß╗Żc.
b) Thß╗Ł lß║Īi c├Īc gi├Ī trß╗ŗ t├¼m ─æŲ░ß╗Żc ß╗¤ c├óu a c├│ thß╗Åa m├Żn phŲ░ŲĪng tr├¼nh ─æ├Ż cho hay kh├┤ng.
-
Luyß╗ćn tß║Łp 1 trang 25 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt{3x^{2}-6x+1}=\sqrt{-2x^{2}-9x+1}\)
b) \(\sqrt{2x^{2}-3x-5}=\sqrt{x^{2}-7}\)
-
Hoß║Īt ─æß╗Öng 2 trang 25 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho phŲ░ŲĪng tr├¼nh \(\sqrt{26x^{2}-63x+38}= 5x-6\)
a) B├¼nh phŲ░ŲĪng hai vß║┐ v├Ā giß║Żi phŲ░ŲĪng tr├¼nh nhß║Łn ─æŲ░ß╗Żc.
b) Thß╗Ł lß║Īi c├Īc gi├Ī trß╗ŗ x t├¼m ─æŲ░ß╗Żc ß╗¤ c├óu a c├│ thß╗Åa m├Żn phŲ░ŲĪng tr├¼nh ─æ├Ż cho hay kh├┤ng.
-
Luyß╗ćn tß║Łp 2 trang 26 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt{2x^{2}+x+3}= 1-x\)
b) \(\sqrt{3x^{2}-13x+14}= x-3\)
-
Vß║Łn dß╗źng trang 26 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
B├Īc Viß╗ćt sß╗æng v├Ā l├Ām viß╗ćc tß║Īi trß║Īm hß║Żi ─æ─āng c├Īch bß╗Ø biß╗ān 4 km. Hß║▒ng tuß║¦n b├Īc ch├©o thuyß╗ün v├Āo vß╗ŗ tr├Ł gß║¦n nhß║źt tr├¬n bß╗Ø biß╗ān l├Ā bß║┐n B├Łnh ─æß╗ā nhß║Łn h├Āng h├│a do cŲĪ quan cung cß║źp. Tuß║¦n n├Āy, do trß╗źc trß║Ęc vß╗ü vß║Łn chuyß╗ān n├¬n to├Ān bß╗Ö sß╗æ h├Āng vß║½n nß║▒m ß╗¤ th├┤n Ho├Ānh, b├¬n bß╗Ø biß╗ān c├Īch bß║┐n B├Łnh 9,25 km v├Ā sß║Į ─æŲ░ß╗Żc anh Nam vß║Łn chuyß╗ān tr├¬n con ─æŲ░ß╗Øng dß╗Źc bß╗Ø biß╗ān tß╗øi bß║┐n B├Łnh bß║▒ng xe k├®o. B├Īc Viß╗ćt ─æ├Ż gß╗Źi ─æiß╗ćn thß╗æng nhß║źt vß╗øi anh Nam l├Ā hß╗Ź sß║Į gß║Ęp nhau ß╗¤ vß╗ŗ tr├Ł n├Āo ─æ├│ giß╗»a bß║┐n B├Łnh v├Ā th├┤n Ho├Ānh ─æß╗ā hai ngŲ░ß╗Øi c├│ mß║Ęt tß║Īi ─æ├│ c├╣ng l├║c, kh├┤ng mß║źt thß╗Øi gian chß╗Ø nhau. T├¼m vß╗ŗ tr├Ł hai ngŲ░ß╗Øi dß╗▒ ─æß╗ŗnh gß║Ęp nhau, biß║┐t rß║▒ng vß║Łn tß╗æc k├®o xe cß╗¦a anh nam l├Ā 5 km/h v├Ā thuyß╗ün cß╗¦a b├Īc Viß╗ćt di chuyß╗ān vß╗øi vß║Łn tß╗æc 4 km/h. Ngo├Āi ra giß║Ż thiß║┐t rß║▒ng ─æŲ░ß╗Øng bß╗Ø biß╗ān tß╗½ th├┤n Ho├Ānh ─æß║┐n bß║┐n B├Łnh l├Ā ─æŲ░ß╗Øng thß║│ng v├Ā b├Īc Viß╗ćt c┼®ng lu├┤n ch├©o thuyß╗ün tß╗øi mß╗Öt ─æiß╗ām tr├¬n bß╗Ø biß╗ān theo mß╗Öt ─æŲ░ß╗Øng thß║│ng.
-
Giß║Żi b├Āi 6.20 trang 27 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt{3x^{2}-4x-1}=\sqrt{2x^{2}-4x+3}\)
b) \(\sqrt{x^{2}+2x-3}=\sqrt{-2x^{2}+5}\)
c) \(\sqrt{2x^{2}+3x-3}=\sqrt{-x^{2}-x+1}\)
d) \(\sqrt{-x^{2}+5x-4}=\sqrt{-2x^{2}+4x+3}\)
-
Giß║Żi b├Āi 6.21 trang 27 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt{6x^{2}+13x+13}=2+4\)
b) \(\sqrt{2x^{2}+5x+3}=-3-x\)
c) \(\sqrt{3x^{2}-17x+23}=x-3\)
d) \(\sqrt{-x^{2}+2x+4}=x-2\)
-
Giß║Żi b├Āi 6.22 trang 27 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho tß╗® gi├Īc ABCD c├│ AB \(\bot \) CD; AB = 2; BC = 13; CD = 8; DA = 5. Gß╗Źi H l├Ā giao ─æiß╗ām cß╗¦a AB v├Ā CD v├Ā ─æß║Ęt x = AH. H├Ży thiß║┐t lß║Łp mß╗Öt phŲ░ŲĪng tr├¼nh ─æß╗ā t├Łnh ─æß╗Ö d├Āi x, tß╗½ ─æ├│ t├Łnh diß╗ćn t├Łch tß╗® gi├Īc ABCD.
-
Giß║Żi b├Āi 6.23 trang 27 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Hß║▒ng ng├Āy bß║Īn H├╣ng ─æß╗üu ─æ├│n bß║Īn Minh ─æi hß╗Źc tß║Īi mß╗Öt vß╗ŗ tr├Ł tr├¬n lß╗ü ─æŲ░ß╗Øng thß║│ng ─æß║┐n trŲ░ß╗Øng. Minh ─æß╗®ng tß║Īi vß╗ŗ tr├Ł A c├Īch lß╗ü ─æŲ░ß╗Øng mß╗Öt khoß║Żng 50 m ─æß╗ā chß╗Ø H├╣ng. Khi nh├¼n thß║źy H├╣ng ─æß║Īp xe ─æß║┐n ─æß╗ŗa ─æiß╗ām B, c├Īch m├¼nh mß╗Öt ─æoß║Īn 200 m th├¼ Minh bß║»t ─æß║¦u ─æi bß╗Ö ra lß╗ü ─æŲ░ß╗Øng ─æß╗ā bß║»t kß╗ŗp xe. Vß║Łn tß╗æc ─æi bß╗Ö Minh l├Ā 5 km/h, vß║Łn tß╗æc xe ─æß║Īp cß╗¦a H├╣ng l├Ā 15 km/h. H├Ży x├Īc ─æß╗ŗnh vß╗ŗ tr├Ł C tr├¬n lß╗ü ─æŲ░ß╗Øng ─æß╗ā hai bß║Īn gß║Ęp nhau m├Ā kh├┤ng bß║Īn n├Āo phß║Żi chß╗Ø ngŲ░ß╗Øi kia (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n h├Āng phß║¦n mŲ░ß╗Øi).
-
Giß║Żi b├Āi 6.28 trang 21 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt { - {x^2} + 77x - 212} = \sqrt {{x^2} + x - 2} \)
b) \(\sqrt {{x^2} + 25x - 26} = \sqrt {x - {x^2}} \)
c) \(\sqrt {4{x^2} + 8x - 37} = \sqrt { - {x^2} - 2x + 3} \)
-
Giß║Żi b├Āi 6.29 trang 21 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt {2{x^2} - 13x + 16} = 6 - x\)
b) \(\sqrt {3{x^2} - 33x + 55} = x - 5\)
c) \(\sqrt { - {x^2} + 3x + 1} = x - 4\)
-
Giß║Żi b├Āi 6.30 trang 21 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Giß║Żi c├Īc phŲ░ŲĪng tr├¼nh sau:
a) \(\sqrt {2x - 3} = x - 3\)
b) \((x - 3)\sqrt {{x^2} + 4} = {x^2} - 9\)
-
Giß║Żi b├Āi 6.31 trang 21 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
T├¼m ─æiß╗üu kiß╗ćn cß╗¦a tham sß╗æ m ─æß╗ā phŲ░ŲĪng tr├¼nh sau c├│ nghiß╗ćm: \(\sqrt {2{x^2} + x + 1} = \sqrt {{x^2} + mx + m - 1} \) (1)
-
Giß║Żi b├Āi 6.32 trang 21 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
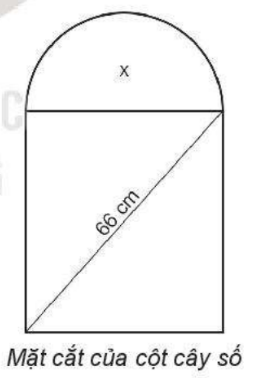
Mß║Ęt cß║»t ─æß╗®ng cß╗¦a cß╗Öt c├óy sß╗æ tr├¬n quß╗æc lß╗Ö c├│ dß║Īng nß╗Ła h├¼nh tr├▓n ß╗¤ ph├Ła tr├¬n v├Ā ph├Ła dŲ░ß╗øi c├│ dß║Īng h├¼nh chß╗» nhß║Łt (xem h├¼nh b├¬n). Biß║┐t rß║▒ng ─æŲ░ß╗Øng k├Łnh cß╗¦a nß╗Ła h├¼nh tr├▓n c┼®ng l├Ā cß║Īnh ph├Ła tr├¬n cß╗¦a h├¼nh chß╗» nhß║Łt v├Ā ─æŲ░ß╗Øng ch├®o cß╗¦a h├¼nh chß╗» nhß║Łt c├│ ─æß╗Ö d├Āi 66 cm. T├¼m k├Łch thŲ░ß╗øc cß╗¦a h├¼nh chß╗» nhß║Łt, biß║┐t rß║▒ng diß╗ćn t├Łch cß╗¦a phß║¦n nß╗Ła h├¼nh tr├▓n bß║▒ng 0,3 lß║¦n diß╗ćn t├Łch cß╗¦a phß║¦n h├¼nh chß╗» nhß║Łt. Lß║źy \(\pi = 3,14\) v├Ā l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® hai.

.JPG)
.JPG)
.JPG)





