Hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Chương 4 Bài 1 Giá trị lượng giác của một góc từ 0˚ đến 180˚ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khám phá 1 trang 61 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
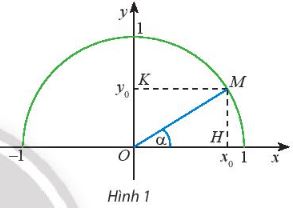
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
\(\sin \alpha = {y_0};\;\cos \alpha = {x_0};\;\tan \alpha = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{{x_0}}}{{{y_0}}}.\)
-
Thực hành 1 trang 62 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tìm các giá trị lượng giác của góc \({135^o}\)
-
Hoạt động khám phá 2 trang 62 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
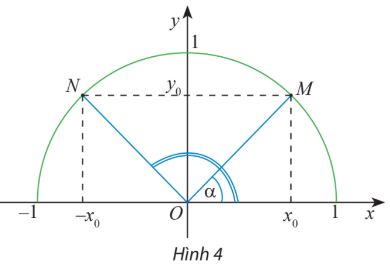
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc \(\widehat {xOM}\) và \(\widehat {xON}.\)
-
Thực hành 2 trang 63 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)
-
Vận dụng 1 trang 63 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho biết \(\sin \alpha = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.
-
Thực hành 3 trang 63 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tính:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
-
Vận dụng 2 trang 64 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tìm góc \(\alpha ({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:
a) \(\sin \alpha = \frac{{\sqrt 3 }}{2}\)
b) \(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\)
c) \(\tan \alpha = - 1\)
d) \(\cot \alpha = - \sqrt 3 \)
-
Thực hành 4 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
a) Tính \(\cos {80^o}43'51'';\tan {147^o}12'25'';\cot {99^o}9'19''.\)
b) Tìm \(\alpha \;({0^o} \le \alpha \le {180^o}),\) biết \(\cos \alpha = - 0,723.\)
-
Giải bài 1 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho biết \(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1.\) Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của \(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)
-
Giải bài 2 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Chứng minh các hệ thức sau:
a) \(\sin {20^o} = \sin {160^o}\)
b) \(\cos {50^o} = - \cos {130^o}\)
-
Giải bài 3 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tìm góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:
a) \(\cos \alpha = - \frac{{\sqrt 2 }}{2}\)
b) \(\sin \alpha = 0\)
c) \(\tan \alpha = 1\)
d) \(\cot \alpha \) không xác định.
-
Giải bài 4 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tam giác ABC. Chứng minh rằng:
a) \(\sin A = \sin \;(B + C)\)
b) \(\cos A = - \cos \;(B + C)\)
-
Giải bài 5 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Chứng minh rằng với mọi góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\), ta đều có:
a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)
c) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)
d) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)
-
Giải bài 6 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho góc \(\alpha \) với \(\cos \alpha = - \frac{{\sqrt 2 }}{2}.\) Tính giá trị của biểu thức \(A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha .\)
-
Giải bài 7 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Dùng máy tính cầm tay, hãy thực hiện các yên cầu dưới đây:
a) Tính \(\sin {168^o}45'33'';\cos {17^o}22'35'';\tan {156^o}26'39'';\cot {56^o}36'42''.\)
b) Tìm \(\alpha \;({0^o} \le \alpha \le {180^o}),\)trong các trường hợp sau:
i) \(\sin \alpha = 0,862.\)
ii) \(\cos \alpha = - 0,567.\)
iii) \(\tan \alpha = 0,334.\)
-
Giải bài 1 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Tính giá trị của \(T = 4\cos 60^\circ + 2\sin 135^\circ + 3\cot 120^\circ \)
-
Giải bài 2 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Chứng minh rằng
a) \(\sin 138^\circ = \sin 42^\circ \)
b) \(\tan 125^\circ = - \cot 35^\circ \)
-
Giải bài 3 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Tìm góc \(\alpha \left( {0^\circ \le \alpha \le 180^\circ } \right)\) trong mỗi trường hợp sau:
a) \(\cos \alpha = - \frac{{\sqrt 3 }}{2}\)
b) \(\sin \alpha = \frac{{\sqrt 3 }}{2}\)
c) \(\tan \alpha = - \frac{{\sqrt 3 }}{3}\)
d) \(\cot \alpha = - 1\)
-
Giải bài 4 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Chứng minh rằng trong tam giác ABC ta có:
a) \(\tan B = - \tan \left( {A + C} \right)\)
b) \(\sin C = \sin \left( {A + B} \right)\)
-
Giải bài 5 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Chứng minh rằng với mọi góc \(x\left( {0^\circ \le x \le 90^\circ } \right)\), ta đều có:
a) \(\sin x = \sqrt {1 - {{\cos }^2}x} \)
b) \(\cos x = \sqrt {1 - {{\sin }^2}x} \)
c) \({\tan ^2}x = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\left( {x \ne 90^\circ } \right)\)
d) \({\cot ^2}x = \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}}\left( {x \ne 0^\circ } \right)\)
-
Giải bài 6 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho góc x với \(\cos x = - \frac{1}{2}\). Tính giá trị của biểu thức \(S = 4{\sin ^2}x + 8{\tan ^2}x\)
-
Giải bài 7 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Dùng máy tính cầm tay, tính:
a) \(\sin 130^\circ 12'24''\)
b) \(\cos 144^\circ 35'12''\)
c) \(\tan 152^\circ 35'44''\)
-
Giải bài 8 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Dùng máy tính cầm tay, tìm x biết:
a) \(\cos x = - 0,234\)
b) \(\sin x = 0,812\)
c) \(\cot x = - 0,333\)