Hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 4 Bài 1 Giá trị lượng giác của một góc từ 0˚ đến 180˚ - định lí côsin và định lí sin trong tam giác giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động 1 trang 63 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC vuông tại A có \(\widehat {ABC} = \alpha \) (Hình 2).
a) Nhắc lại định nghĩa sin α, cos α, tan α, cot α.
b) Biểu diễn tỉ số lượng giác của góc 90° – α theo tỉ số lượng giác của góc α.
-
Hoạt động 2 trang 63 SGK Toán 10 Cánh diều tập 1 - CD
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (Hình 3). Với mỗi góc nhọn α ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Giả sử điểm M có tọa độ (x0; y0). Hãy tính sin α, cos α, tan α, cot α theo x0, y0.
-
Hoạt động 3 trang 64 SGK Toán 10 Cánh diều tập 1 - CD
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và \(\widehat {xOM} = \alpha \).
a) Chứng minh \(\widehat {xON} = {180^o} - \alpha \)
b) Biểu diễn giá trị lượng giác của góc \({180^o} - \alpha \) theo giá trị lượng giác của góc \(\alpha \).
-
Hoạt động 4 trang 66 SGK Toán 10 Cánh diều tập 1 - CD
Ta có thể tìm giá trị lượng giác (đúng hoặc gần đúng) của một góc (từ 0° đến 180°) bằng cách sử dụng các phím:
trên máy tính cầm tay.
Tính sin75°, cos175°, tan64° (làm tròn đến hàng phần chục nghìn).
-
Hoạt động 5 trang 66 SGK Toán 10 Cánh diều tập 1 - CD
Ta có thể tìm số đo (đúng hoặc gần đúng) của một góc từ 0° đến 180° khi biết giá trị lượng giác của góc đó bằng cách sử dụng các phím:
cùng với
trên máy tính cầm tay.
Tìm số đo góc α (từ 0° đến 180°) và làm tròn đến độ, biết:
a) cos α = – 0,97;
b) tan α = 0,68;
c) sin α = 0,45.
-
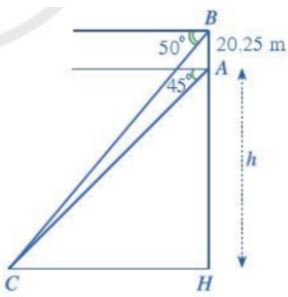
Luyện tập 1 trang 66 SGK Toán 10 Cánh diều tập 1 - CD
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
-
Hoạt động 6 trang 67 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có BC = a, AC = b, AB = c, \(\widehat {BAC} = \alpha \). Kẻ đường cao BH. Cho α là góc nhọn, chứng minh:
a) HC = |AC – AH| và BC2 = AB2 + AC2 – 2AH . AC;
b) a2 = b2 + c2 – 2bc cos α.
-
Hoạt động 7 trang 67 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có BC = a, AC = b, AB = c, \(\widehat {BAC} = \alpha \). Kẻ đường cao BH Cho α là góc tù. Chứng minh:
a) HC = AC + AH và BC2 = AB2 + AC2 + 2 AH . AC;
b) a2 = b2 + c2 – 2bc cos α.
-
Hoạt động 8 trang 68 SGK Toán 10 Cánh diều tập 1 - CD
Cho \(\alpha \) là góc vuông. Chứng minh \({a^2} = {b^2} + {c^2} - 2bc.\cos \alpha \)
-
Luyện tập 2 trang 68 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có AB = 5, AC = 6, BC =7. Tính cosA.
-
Hoạt động 9 trang 69 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, \(\widehat {BAC} = \alpha \). Kẻ đường kính BD của đường tròn (O).
Cho α là góc nhọn. Chứng minh:
a) \(\widehat {BDC} = \alpha \);
b) \(\frac{a}{{\sin \alpha }} = 2R\).
-
Hoạt động 10 trang 69 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, \(\widehat {BAC} = \alpha \). Kẻ đường kính BD của đường tròn (O).
Cho α là tù. Chứng minh:
a) \(\widehat {BDC} = 180^\circ - \alpha \);
b) \(\frac{a}{{\sin \alpha }} = 2R.\)
-
Hoạt động 11 trang 70 SGK Toán 10 Cánh diều tập 1 - CD
Cho \(\alpha \) là góc vuông. Chứng minh \(\frac{a}{{\sin \alpha }} = 2R.\)
-
Luyện tập 3 trang 70 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc \(\widehat B = {65^o},\widehat C = {85^o}.\) Tính độ dài cạnh BC.
-
Giải bài 1 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
-
Giải bài 2 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(\widehat B = {75^o},\widehat C = {45^o}\) và BC = 50. Tính độ dài cạnh AB.
-
Giải bài 3 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 6,AC = 7,BC = 8\). Tính \(\cos A,\sin A\) và bán kính R của đường trong ngoại tiếp tam giác ABC.
-
Giải bài 4 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Tính giá trị đúng của các biểu thức sau (không dùng máy tính cầm tay):
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
-
Giải bài 5 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC. Chứng minh:
a) \(\sin \frac{A}{2} = \cos \frac{{B + C}}{2}\)
b) \(\tan \frac{{B + C}}{2} = \cot \frac{A}{2}\)
-
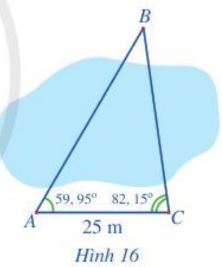
Giải bài 6 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\) Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
-
Giải bài 7 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc \({75^o}\). Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?
-
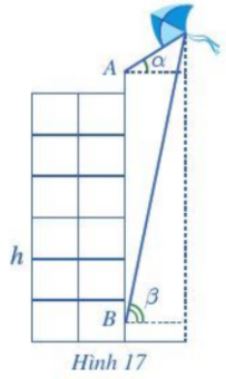
Giải bài 8 trang 71 SGK Toán 10 Cánh diều tập 1 - CD
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là \(\alpha = {35^o}\); khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là \(\beta = {75^o}\); khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?
-
Giải bài 1 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho 00 < \(\alpha \) < 1800. Chọn câu trả lời đúng
A. cos\(\alpha \) < 0
B. sin\(\alpha \) > 0
C. tan\(\alpha \) < 0
D. cot\(\alpha \) > 0
-
Giải bài 2 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho 00 < \(\alpha \), \(\beta \) < 1800 và \(\alpha + \beta = {180^0}\). Chọn câu trả lời sai
A. \(\sin \alpha + \sin \beta = 0\)
B. \(\cos \alpha + \cos \beta = 0\)
C. \(\tan \alpha + \tan \beta = 0\)
D. \(\cot \alpha + \cot \beta = 0\)
-
Giải bài 3 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Tính giá trị của biểu thức \(T = {\sin ^2}{25^0} + {\sin ^2}{75^0} + {\sin ^2}{115^0} + {\sin ^2}{165^0}\)
-
Giải bài 4 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho \(\tan \alpha = - 2\). Tính giá trị biểu thức \(P = \frac{{\cos \alpha + 3\sin \alpha }}{{\sin \alpha + 3\cos \alpha }}\)
-
Giải bài 5 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 6,AC = 8,\widehat A = {100^0}\). Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười)
-
Giải bài 6 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(\widehat B = {60^0},\widehat C = {105^0}\) và \(BC = 15\). Tính độ dài cạnh AC và bán kính R của đường tròn ngoại tiếp tam giác ABC (làm tròn kết quả đến hàng phần mười)
-
Giải bài 7 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 5,AC = 7,BC = 9\). Tính số đo góc A và bán kính R của đường tròn ngoại tiếp tam giác ABC (làm tròn kết quả đến hàng phần mười)
-
Giải bài 8 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\)
-
Giải bài 9 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Từ một tấm tôn hình tròn bán kính R = 1 m, bạn trí muốn cắt ra một hình tam giác ABC có các góc A = 450, B = 750. Hỏi bạn Trí phải cắt miếng tôn theo hai dây cung AB, BC có độ dài lần lượt bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
-
Giải bài 10 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Một cây cao bị nghiêng so với mặt đất góc 780. Từ vị trí C cách gốc cây 20 m, người ta tiến hành đo đạc và thu được kết quả \(\widehat {ACB} = {50^0}\) với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét)
-
Giải bài 11 trang 75 SBT Toán 10 Cánh diều tập 1 - CD
Tàu A cách cảng C một khoảng 3 km và lệch hướng bắc một góc 47,450. Tàu B cách cảng C một khoảng 5 km và lệch hướng bắc một góc 112,900 (Hình 11). Hỏi khoảng cách giữa hai tàu là bao nhiêu kilomet (làm tròn kết quả đến hàng phần trăm)?

.JPG)
.JPG)