-
Đáp án A
Đặc điểm cơ bản của địa hình Trung Quốc là thấp dần từ tây sang đông (hình 10.1 sgk Địa lí 11 trang 87). Vì miền Tây Trung Quốc địa hình chủ yếu là các sơn nguyên, các dãy núi cao, càng về phía Đông độ cao càng giảm dần và ven biển là các đồng bằng thấp
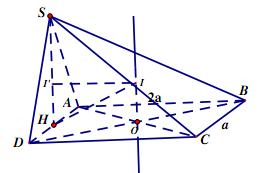
Câu hỏi:Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB=2a, BC=a, hình chiếu của S lên (ABCD) là trung điểm H của AD, \(SH = \frac{{a\sqrt 3 }}{2}.\) Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng bao nhiêu?
- A. \(\frac{{16\pi {a^2}}}{3}\).
- B. \(\frac{{16\pi {a^2}}}{9}\).
- C. \(\frac{{4\pi {a^3}}}{3}\).
- D. \(\frac{{4\pi {a^2}}}{3}\).
Đáp án đúng: A
Gọi I’ là tâm đường tròn ngoại tiếp tam giác SAD.
O là tâm đường tròn ngoại tiếp ABCD.
Đường thẳng qua O vuông góc với (ABCD) là trục đường tròn ngoại tiếp hình vuông ABCD.
Mặt phẳng qua I’ cắt trục đường tròn ngoại tiếp hình vuông ABCD tại I.
Ta có I chính làm tâm mặt cầu ngoại tiếp khối chóp S.ABCD.
Dễ thấy OHI’I là hình chữ nhật.
Ta có \(SD = SA = \sqrt {S{H^2} + A{H^2}} = a\) suy ra tam giác SAD đều.
\(\begin{array}{l} \Rightarrow I'A = \frac{2}{3}\frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{3}a\\ \Rightarrow R = IA = \sqrt {I'{A^2} + I'{I^2}} = \sqrt {I'{A^2} + H{O^2}} = \frac{{2a}}{{\sqrt 3 }} \end{array}\)
Vậy \(S = 4\pi {R^2} = \frac{{16\pi {a^2}}}{3}.\)
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ MẶT CẦU, DIỆN TÍCH MẶT CẦU, THỂ TÍCH KHỐI CẦU
- Tính bán kính R của mặt cầu ngoại tiếp hình chóp đều S.ABC có cạnh đáy bằng a, góc tạo bởi cạnh bên và đáy bằng 60 độ
- Tính thể tích V của khối lập phương biết hình cầu có thể tích {8sqrt 2pi }/{3} nội tiếp trong một hình lập phương.
- Tính thể tích của khối cầu ngoại tiếp một khối lập phương có cạnh bằng a
- Tính diện tích S của mặt cầu đi qua các đỉnh của hình lập phương có cạnh bằng 1
- Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát bằng thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau.
- Tính bán kính R của mặt cầu ngoại tiếp tứ diện AB’C’C biết lăng trụ đứng ABC.A’B’C’ có AB = AC = a,BC = asqrt 3. Cạnh bên AA’=2a.
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 căn 2 cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3 mặt phẳng (alpha ) qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M,N,P
- Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC biết hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC=120 độ
- Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC=2a. SA vuông góc với mặt đáy và
- Tính diện tích S của mặt cầu ngoại tiếp hình chóp S.ABC biết khối chóp S.ABC có đáy là tam giác vuông tại A, AB=a, AC=2a