Tìm tất cả giá trị của tham số m để hàm số y=(x^2-4x)/(x+m) đồng biến trên [1;+ vô cực]

Xét hàm số \(y = \frac{{{x^2} - 4x}}{{x + m}},\) ta có:

 \(y' = \frac{{(2x - 4)(x + m) - {x^2} + 4x}}{{{{(x + m)}^2}}} = \frac{{{x^2} + 2mx - 4m}}{{{{(x + m)}^2}}},\forall x \ne - m\)

Hàm số đồng biến trên \({\rm{[}}1; + \infty )\) khi và chỉ khi \(\left\{ \begin{array}{l} y' \ge 0,\forall x \in \left[ {1; + \infty } \right)(*)\\ x = - m \notin \forall x \in \left[ {1; + \infty } \right) \Leftrightarrow m > - 1 \end{array} \right.\)

Ta có (*) \(\Rightarrow {x^2} + 2mx - 4m \ge 0 \Leftrightarrow {x^2} \ge 2m(2 - x)(I)\)

+ TH1. Với x = 2 \(\Rightarrow {x^2} \ge 0,\forall x \in \left[ {1; + \infty } \right)\) với mọi giá trị của m

+ TH2. Với \(2 - x > 0 \Leftrightarrow x < 2 \Rightarrow x \in {\rm{[}}1;2)\).

Khi đó (I)\(\Leftrightarrow 2m \le \frac{{{x^2}}}{{2 - x}};\forall x \in {\rm{[}}1;2) \Rightarrow 2m \le \mathop {m{\rm{in}}}\limits_{{\rm{[}}1;2)} {\rm{f}}(x)\)  

+ TH3. Với \(2 - x < 0 \Leftrightarrow x > 2 \Rightarrow x \in \left( {2; + \infty } \right)\)

 Khi đó (I)\(\Leftrightarrow 2m \ge \frac{{{x^2}}}{{2 - x}};\forall x \in (2; + \infty ) \Rightarrow 2m \ge \mathop {\max }\limits_{\left( {2; + \infty } \right)} {\rm{f}}(x)\) 

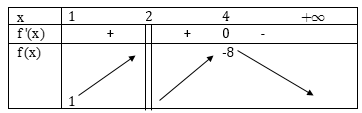
Xét hàm số \(f(x) = \frac{{{x^2}}}{{2 - x}},\) ta có \(f'(x) = - \frac{{x(x - 4)}}{{{{(2 - x)}^2}}};\forall x \ne 2\)  

\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 4 \end{array} \right.\)

\(\Rightarrow \left\{ \begin{array}{l} \mathop {\min }\limits_{{\rm{[}}1;2)} f(x) = f(1) = 1\\ \mathop {\max }\limits_{(2; + \infty )} f(x) = f(4) = - 8 \end{array} \right.\)

Kết hợp các trường hợp, ta được \(- 1 < m \le \frac{1}{2}\) là giá trị cần tìm.