-
Câu hỏi:
Cho hàm số f(x)=14x4−2x3+3f(x)=14x4−2x3+3. Kết luận nào sau đây là đúng?
- A. Cực đại hàm số bằng 33.
- B. Cực đại hàm số bằng 33.
- C. Hàm số đồng biến trên khoảng (0;+∞)(0;+∞).
- D. Đồ thị của hàm số có 22 cực trị.
Đáp án đúng: A
TXĐ:
D=R
f′(x)=x4−4x=x(x2−4).
Giải f′(x)=0⇔x(x2−4)⇔[x=0x=±2
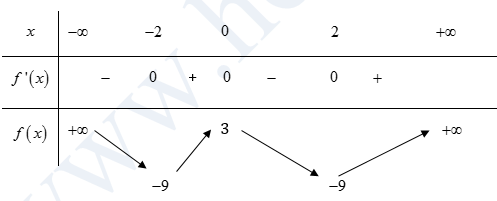
Bảng biến thiên:
Vậy cực đại của hàm số bằng 3.
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ CỰC TRỊ CỦA HÀM SỐ
- Cho hàm số y = {x^3} + {x^2} + mx + 1, tìm các giá trị thực của tham số(m)để hàm số có hai điểm cực trị nằm về 2 phía của trục tung
- Cho hàm số f có đạo hàm trên khoảng (left( {a;b} ight)) chứa ({x_0},f'left( {{x_0}} ight) = 0) và f có đạo hàm cấp hai tại {x_0}
- Cho hàm số y = xln {x}. Chọn khẳng định đúng trong các khẳng định sau:
- Hàm số y = - {x^4} + 2{{{x}}^2} - 3 có điểm cực đại {x_{Cđ}} và điểm cực tiểu {x_{CT} là:
- Cho hàm số y=sinx+cosx-sqrt3 x Chọn khẳng định đúng trong các khẳng định sau:
- Cho hàm số y=f(x) liên tục trên đoạn [-2;3], có bảng biến thiên như hình vẽ bên
- Hàm số y = sin x đạt cực đại tại điểm nào sau đây?
- Cho hàm số y=f(x) liên tục và có đạo hàm cấp hai trên (mathbb{R}). Đồ thị của các hàm số y=f(x), y=f′(x), y=f''(x) lần lượt là các đường cong nào trong hình vẽ bên
- Cho hàm số y=f(x) xác định, liên tục trên đoạn [-1;3] và có đồ thị là đường cong như hình vẽ.
- Cho hàm số y=x^2−3x+1/x có giá trị cực đại {y_1} và giá trị cực tiểu {y_2}.