-
Câu hỏi:
Cho hàm số có bảng biến thiên sau:
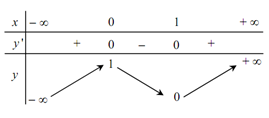
Phát biểu nào sau đây là đúng.- A. Hàm số đồng biến trên\(( - \infty ;0) \cup \left( {1; + \infty } \right)\) và nghịch biến trên (0;1)
- B. Hàm số đồng biến trên hai khoảng \(( - \infty ;1);\left( {0; + \infty } \right)\) và nghịch biến trên (0;1)
- C. Hàm số đồng biến trên hai khoảng \((- \infty ;0);\left( {1; + \infty } \right)\) và nghịch biến trên (0; 1)
- D. Hàm số đồng biến trên \(\mathbb{R} \setminus \left( {0;1} \right)\) và nghịch biến trên (0; 1)
Lời giải tham khảo:
Đáp án đúng: C
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong các phát biểu sau, phát biểu nào đúng?
- Hàm số đồng biến trên\(( - \infty ;0) \cup \left( {1; + \infty } \right)\) và nghịch biến trên (0;1)
- Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {11; + \infty } \right)\) và nghịch biến trên (-1; 11)
- Hàm số f(x) có đạo hàm \(f(x) = {x^2}(x + 2)\) Phát biểu nào sau đây là đúng?
- Hàm số \(y = - {x^3} - 3{x^2} - 4\) đồng biến trên khoảng nào sau đây:
- Tìm m để hàm số y=mx-3/x+1 đồng biến trên từng khoảng xác định
- Nếu x0 là nghiệm của f'(x) = 0 thì hàm số f(x) đạt cực trị tại x0
- Hàm số f(x) có đạo hàm \(f(x) = {x^2}{(x + 1)^2}\). Số cực trị của hàm số là
- Hàm số f(x) có đạo hàm \(f(x) = {x^2}{(x + 1)^2}(x + 2).\) Phát biểu nào sau đây là đúng:
- Giá trị cực đại của hàm số \(y = {x^3} - 3x + 2\) là:
- Hàm số đạt cực tiểu tại x = -1 và đạt cực đại tại x = 3
- Điểm cực đại của đồ thị hàm số \(y = \frac{1}{2}{x^4} - 2{x^2} - 3\) là:
- Cho hàm số có bảng biến thiên sauTrong các khẳng định sau khẳng định nào đúng?
- Cho hàm số \(y = \frac{{x + 1}}{{\sqrt {{x^2} - 1} }}.\) Số tiệm cận ngang của đồ thị hàm số là:
- Cho hàm số \(y = \frac{{2x - 3}}{{x + 1}}\). Giao điểm hai đường tiệm cận của đồ thị hàm số có tọa độ là:
- Cho hàm số \(y = {x^3} + 5x + 7.\) Giá trị lớn nhất của hàm số trên đoạn [-5; 0] là:
- Giá trị lớn nhất của hàm số là 2.
- Giá trị nhỏ nhất của hàm số \(y = \sin x - \frac{4}{3}{\sin ^3}x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \r
- Cho biểu thức \(A = \frac{{2xy}}{{{x^2} + {y^2}}},\) với \(x, y\neq 0\) Giá trị nhỏ nhất của A bằng:
- Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật, đáy là hình vuông và thể tích khối hộp đượ







