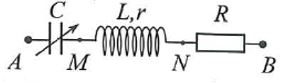
-
Câu hỏi:
Đặt điện áp \(u = 120\cos \left( {100\pi t - \frac{\pi }{6}} \right)\,\,(V)\) vào hai đầu đoạn mạch AB mắc nối tiếp gồm: tụ điện có điện dung C thay đổi được; cuộn dây có độ tự cảm L và điện trở r; điện trở R với R=2r như hình bên.
Khi C=C0 thì điện áp hiệu dụng giữa hai đầu đoạn mạch AN đạt cực tiểu. Khi \(C = \frac{{{C_0}}}{4}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch AM đạt cực đại và điện áp giữa hai đầu đoạn mạch MN là \({u_{{\rm{MN}}}}\). Biểu thức \({u_{{\rm{MN}}}}\) là:
- A. \({u_{{\rm{MN}}}} = 40{\rm{cos}}\left( {100\pi t + \frac{{2\pi }}{3}} \right)\left( {\rm{V}} \right)\)
- B. \({u_{{\rm{MN}}}} = 40\sqrt 3 {\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)\left( {\rm{V}} \right)\)
- C. \({u_{{\rm{MN}}}} = 40\sqrt 3 {\rm{cos}}\left( {100\pi t + \frac{{2\pi }}{3}} \right)\left( {\rm{V}} \right)\)
- D. \({u_{{\rm{MN}}}} = 40{\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)\left( {\rm{V}} \right)\)
Lời giải tham khảo:
Đáp án đúng: D
Chọn D.
Khi C = Co
\({U_{AN}} = \frac{{U\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = min\)
Ta có:
\({U_{AN}} = \frac{U}{{\sqrt {1 + \frac{{{R^2} + 2Rr}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}} }}\;\left( 1 \right)\)
\(\left( 1 \right) \Rightarrow {U_{AN}} = min\) khi
\({Z_C} = {Z_L}\)
\(\Rightarrow {Z_L} = {Z_{C0}}\;\left( 2 \right)\)
Khi \(C = \frac{{{C_0}}}{4}\) thì \({Z_C} = 4{Z_{C0}}\)
\({U_{AM}} = {U_C} = max\)
\(\Rightarrow \;{Z_C} = \frac{{{{\left( {R + r} \right)}^2} + Z_L^2}}{{{Z_L}}}\)
\(\left( {4{Z_{C0}}} \right) = \frac{{{{\left( {2r + r} \right)}^2} + {{\left( {{Z_{C0}}} \right)}^2}}}{{\left( {{Z_{C0}}} \right)}}\)
\(\Rightarrow \left\{ {\begin{array}{*{20}{c}} {r = \frac{{{Z_{C0}}}}{{\sqrt 3 }}}\\ {R = \frac{{2{Z_{C0}}}}{{\sqrt 3 }}} \end{array}} \right.\)
Phương trình điện áp hai đầu đoạn mạch MN (phức hóa)
\(\overline {{u_{MN}}} = \frac{{\overline {u\;} }}{{\overline {Z\;} }}.\overline {{Z_{MN}}} \)
\(\overline {{u_{MN}}} = \frac{{\left( {120\angle - \frac{\pi }{6}} \right)}}{{\left[ {\left( {\sqrt 3 } \right) + \left( {1 - 4} \right)i} \right]}}.\left[ {\left( {\frac{1}{{\sqrt 3 }}} \right) + \left( 1 \right)i} \right] = 40\angle \frac{\pi }{2}\)
Vậy \({u_{MN}} = 40{\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)V\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu một đoạn mạch chỉ có cuộn cảm thuần
- Một vật dao động điều hòa dọc trục Ox
- Theo thuyết lượng tử ánh sáng, mỗi lần một nguyên tử hay phân tử phát xạ ánh sáng thì chúng phát ra
- Chu kì bán rã T của chất phóng xạ này được tính bằng công thức nào sau đây?
- Hai dao động điều hòa cùng tần số có pha ban đầu
- Trong sơ đồ khối của một máy thu thanh vô tuyến đơn giản không có bộ phận nào sau đây
- Xét một tia sáng đi từ môi trường có chiết suất n1 sang môi truờng có chiết suất n2 nhỏ hơn.
- Một mạch dao động LC lí tưởng đang dao động điện từ tự do
- Một con lắc đơn có chiều dài l, vật nhỏ khối lượng m
- Tia X có cùng bản chất với tia nào
- Hai điện tích điểm gây ra tại điểm M hai điện trường
- Hiện tượng tán sắc ánh sáng giúp ta giải thích được hiện tượng nào sau đây?
- Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang.
- Một sóng cơ có chu kỳ T, lan truyền trong một môi truờng với tốc độ v.
- Một vật dẫn đang có dòng điện một chiều chạy qua.
- Số nuclôn có trong hạt nhân là
- Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số góc thay đổi được vào hai đầu một đoạn mạch
- Âm có tần số nằm trong khoảng từ 16Hz đến 20000Hz được gọi là
- Cấu tạo của máy phát điện xoay chiều một pha gồm hai bộ phận chính là
- Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch có R, L, C mắc nối tiếp
- Một sợi dây mềm PQ căng ngang có đầu Q gắn chặt vào tường.
- Theo mẫu nguyên tử Bo, nếu nguyên tử đang ở trạng thái dừng
- Một khung dây dẫn phẳng, kín được đặt trong từ trường đều.
- Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc, khoảng vân đo được trên màn quan sát là 0,08mm.
- Hạt nhân có năng lượng liên kết riêng là 8,8MeV/ nuclôn.
- Ở một nơi trên mặt đất, con lắc đơn có chiều dài l dao động điều hòa với chu kì T.
- Mạch chọn sóng ở một máy thu thanh là mạch dao động
- Đặt một điện áp xoay chiều có tần số góc vào hai đầu đoạn mạch chỉ có cuộn cảm thuần
- Năng lượng cần thiết (năng lượng kích hoạt) để giải phóng một êlectron liên kết thành êlectron dẫn của PbS là:
- Một sợi dây mềm có hai đầu cố định.
- Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số không đổi vào hai đầu đoạn mạch
- Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe cách nhau 0,5mm
- Ở một nơi trên mặt đất, hai con lắc đơn có chiều dài l và l+45 (cm) cùng được kích thích để dao động điều hòa
- rong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại A và B cách nhau 9,6 cm
- Đặt điện áp xoay chiều u vào hai đầu đoạn mạch mắc nối tiếp
- Một nguồn phát ra bức xạ đơn sắc với công suất 50mV.
- M là một phần tử dây ở điểm bụng.
- Pôlôni là chất phóng xạ có chu kì bán rã 138 ngày và biến đổi thành hạt nhân chì
- Ban đầu, giữ m1 ở vị trí lò xo bị nén 7,1 cm
- Đặt điện áp vào hai đầu đoạn mạch AB mắc nối tiếp