-
Câu hỏi:
Cho hàm số \(y=f(x)\) xác định và liên tục trên đoạn \(\left[ {0;\frac{7}{2}} \right]\), có đồ thị của hàm số \(y=f'(x)\) như hình vẽ. Hỏi hàm số \(y=f(x)\) đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;\frac{7}{2}} \right]\) tại điểm \(x_0\) nào dưới đây?
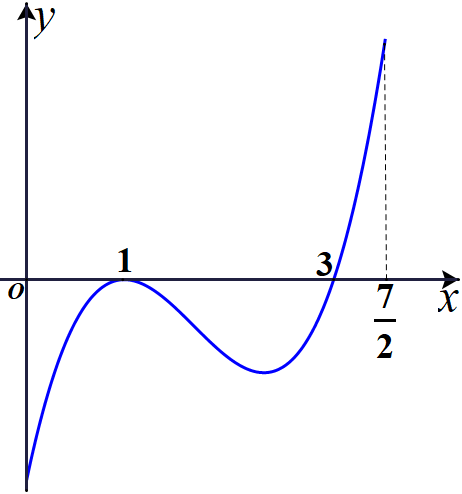
- A. \(x_0=0\)
- B. \(x_0=1\)
- C. \(x_0=3\)
- D. \(x_0=2\)
Lời giải tham khảo:
Đáp án đúng: C
Ta có \(y=f(x)\) xác định và liên tục trên \(\left[ {0;\frac{7}{2}} \right]\) và \(f'\left( x \right) \le 0,\forall x \in \left[ {0;3} \right]\); \(f'\left( x \right) > 0,\forall x \in \left( {3;\frac{7}{2}} \right]\) suy ra hàm số \(y=f(x)\) có duy nhất một cực tiểu tại điểm \(x_0=3\)
\( \Rightarrow \mathop {\min }\limits_{\left[ {0;\frac{7}{2}} \right]} f\left( x \right) = f\left( 3 \right)\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Số nghiệm của phương trình \({\log _3}\left( {{x^2} + 4x} \right) + {\log _{\frac{1}{3}}}\left( {2x + 3} \right) = 0\) là
- Giá trị nhỏ nhất, lớn nhất của hàm số \(y = x - \ln x\) trên đoạn \(\left[ {\frac{1}{2};\,{\rm{e}}} \right]\) theo thứ
- Cho \({\log _{12}}27 = a\). Tính \(T = {\log _{36}}24\) theo \(a\).
- Đặt \(a = {\log _2}3,b = {\log _2}5,c = {\log _2}7\). Biểu thức biểu diễn \({\log _{60}}1050\) theo \(a, b, c\) là.
- Cho \(a = {\log _2}5,b = {\log _3}5\). Tính \({\log _{24}}600\) theo \(a, b\).
- Cho phương trình \({\log _5}\left( {{5^x} - 1} \right).{\log _{25}}\left( {{5^{x + 1}} - 5} \right) = 1\).
- Cho 2 số thực dương \(a, b\) thỏa mãn \(\sqrt a \ne b,a \ne 1,{\log _a}b = 2\).
- Cho \({\log _2}m = a\) và \(A = {\log _m}\left( {8m} \right)\) với \(m > 0,m \ne 1\).
- Cho \(x > 0, y>0\) và \(K = {\left( {{x^{\frac{1}{2}}} - {y^{\frac{1}{2}}}} \right)^2}{\left( {1 - 2\sqrt {\frac{y}{x}} + \frac{y}{x
- Cho \(n\) là số nguyên dương và \(a > 0,a \ne 1\).
- Giải phương trình \({\left( {2,5} \right)^{5x - 7}} = {\left( {\frac{2}{5}} \right)^{x + 1}}\).
- Phương trình \({\log _4}{\left( {x + 1} \right)^2} + 2 = {\log _{\sqrt 2 }}\sqrt {4 - x} + {\log _8}{\left( {4 + x} \right)^3}\) có bao
- Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} - 3x + 1} \right) \le 0\) là
- Cho \(a>0, b>0\) và biểu thức \(T = 2{\left( {a + b} \right)^{ - 1}}.{\left( {ab} \right)^{\frac{1}{2}}}.
- Cho \(a>0, b>0\) và \({a^2} + {b^2} = 7ab\). Chọn mệnh đề đúng.
- Cho hàm số \(y = x\left[ {\cos \left( {\ln x} \right) + \sin \left( {\ln x} \right)} \right]\). Khẳng định nào sau đây đúng?
- Nếu (7+4 căn 3)^(a-1) < 7-4 căn 3 thì?
- Rút gọn biểu thức A=căn bậc 3(a^5).a^(7/3)/a^4.căn bậc 7(a^-2)
- Tìm tất cả các giá trị của tham số để hàm số \(y = {\log _2}\left( {{x^2} - 2x + m} \right)\) có tập xác định là R.
- Cho \(a, b, c >1\).
- E. coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi khuẩn E.
- Biết \({\log _a}b = 2\). Giá trị của \({\log _{{a^2}b}}\frac{{{a^4}}}{{b\sqrt b }}\) bằng
- Cho hàm số \(y=f(x)\) xác định và liên tục trên đoạn \(\left[ {0;\frac{7}{2}} \right]\), có đồ thị của hàm số \(y=f(x)\
- Hệ phương trình \(\left\{ \begin{array}{l}{2^{x + y}} = 8\\{2^x} + {2^y} = 5\end{array} \right.\) có bao nhiêu nghiệm?
- Một người gởi 75 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi suất 5,4% một năm.
- Cho hàm số \(y=a^x\) với \(0 < a \ne 1\) có đồ thị (C). Chọn khẳng định sai?
- Cho \({\log _6}45 = a + \frac{{{{\log }_2}5 + b}}{{{{\log }_2}3 + c}}\) với \(a,b,c \in Z\). Tính tổng \(a+b+c\)?
- Tính tổng tất cả các nghiệm của phương trình sau \({3^{2x + 8}} - {4.3^{x + 5}} + 27 = 0\).
- Tìm tất cả các giá trị của tham số \(a\) để phương trình sau có nghiệm duy nhất \({\log _3}{x^2} + a\sqrt {{{\log }_3}{x^
- Tích các nghiệm của phương trình \({\log _{\frac{1}{{\sqrt 5 }}}}\left( {{6^{x + 1}} - {{36}^x}} \right) = - 2\) bằng
- Cho \(f\left( x \right) = {2.3^{{{\log }_{81}}x}} + 3\). Tính \(f(1)\).
- Chọn ngẫu nhiên một số tự nhiên A có bốn chữ số. Gọi N là số thỏa mãn \(3^N=A\).
- Trong thời gian liên tục 25 năm, một người lao động luôn gửi đúng 4.000.
- Gọi \(x, y\) là các số thực dương thỏa mãn điều kiện \({\log _9}x = {\log _6}y = {\log _4}\left( {x + y} \right)\) và \(\
- Tìm các giá trị thực của tham số \(m\) để bất phương trình \({\log _{0,02}}\left( {{{\log }_2}\left( {{3^x} + 1} \right)} \rig
- Số các giá trị nguyên của tham số \(m\) để phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \
- Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \frac{{m\ln x - 2}}{{\ln x - m - 1}}\) nghịch biến trên \(\lef
- Cho hàm số \(y = {x^3} - {x^2} + 2x + 5\) có đồ thị (C).
- Tính giá trị của biểu thức \(P = \log \left( {\tan 1^\circ } \right) + \log \left( {\tan 2^\circ } \right) + \log \left( {\tan 3^\circ } \ri
- Gọi \(a\) là một nghiệm của phương trình \({\left( {26 + 15\sqrt 3 } \right)^x} + 2{\left( {7 + 4\sqrt 3 } \right)^x} - 2{\left( {2 -







