Câu hỏi trắc nghiệm (20 câu):
-
Câu 1: Mã câu hỏi: 21961
Trong các phát biểu sau, phát biểu nào đúng?
- A. Hàm số f(x) nghịch biến trên (a;b) khi và chỉ khi \(f'(x)\leq 0 \ \forall x\in (a;b)\)
- B. Nếu \(f'(x)\leq 0 \ \forall x\in (a;b)\) thì hàm số f(x) nghịch biến trên (a;b)
- C. Hàm số y= f(x) nghịch biến trên (a;b) khi và chỉ khi \(f'(x)< 0 \ \forall x\in (a;b)\)
- D. Nếu \(f'(x)< 0 \ \forall x\in (a;b)\) thì hàm số y = f(x) nghịch biến trên (a;b)
-
Câu 2: Mã câu hỏi: 21962
Cho hàm số có bảng biến thiên sau:
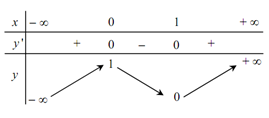
Phát biểu nào sau đây là đúng.- A. Hàm số đồng biến trên\(( - \infty ;0) \cup \left( {1; + \infty } \right)\) và nghịch biến trên (0;1)
- B. Hàm số đồng biến trên hai khoảng \(( - \infty ;1);\left( {0; + \infty } \right)\) và nghịch biến trên (0;1)
- C. Hàm số đồng biến trên hai khoảng \((- \infty ;0);\left( {1; + \infty } \right)\) và nghịch biến trên (0; 1)
- D. Hàm số đồng biến trên \(\mathbb{R} \setminus \left( {0;1} \right)\) và nghịch biến trên (0; 1)
-
Câu 3: Mã câu hỏi: 21963
Cho hàm số có bảng biến thiên sau:
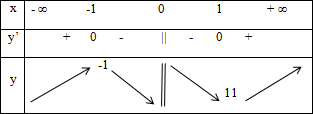
Phát biểu nào sau đây là đúng.- A. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {11; + \infty } \right)\) và nghịch biến trên (-1; 11)
- B. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {1; + \infty } \right)\) và nghịch biến trên (-1; 0); (0; 1)
- C. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {1; + \infty } \right)\) và nghịch biến trên (-1; 1)
- D. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1) \cup \left( {1; + \infty } \right)\) và nghịch biến trên (-1; 0); (0; 1)
-
Câu 4: Mã câu hỏi: 21964
Hàm số f(x) có đạo hàm \(f'(x) = {x^2}(x + 2)\) Phát biểu nào sau đây là đúng?
- A. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right);\left( {0; + \infty } \right)\)
- B. Hàm số đồng biến trên khoảng (-2; 0)
- C. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right);\left( {0; + \infty } \right)\)
- D. Hàm số đồng biến trên khoảng \((-2 ;+\infty )\)
-
Câu 5: Mã câu hỏi: 21965
Hàm số \(y = - {x^3} - 3{x^2} - 4\) đồng biến trên khoảng nào sau đây:
- A. (-2;0)
- B. (-3;0)
- C. \((-\infty ;-2)\)
- D. \((0;+\infty )\)
-
Câu 6: Mã câu hỏi: 21966
Cho hàm số \(y = \frac{{mx - 3}}{{x + 1}}\). Tập hợp giá trị m để hàm số đồng biến trên từng khoảng xác định là:
- A. \(\mathbb{R}\setminus {-3}\)
- B. \((-3;+\infty )\)
- C. \((-\infty ;-3)\)
- D. \(\left \{ 3 \right \}\)
-
Câu 7: Mã câu hỏi: 21967
Trong các phát biểu sau, phát biểu nào đúng?
- A. Nếu x0 là nghiệm của f'(x) = 0 thì hàm số f(x) đạt cực trị tại x0
- B. Nếu hàm số f(x) đạt cực trị tại x0 thì hàm số có đạo hàm tại x0
- C. Hàm số có thể đạt cực trị tại điểm mà tại đó không có đạo hàm.
- D. Nếu hàm số f(x) đạt cực trị tại x0 thì f'(x0) = 0
-
Câu 8: Mã câu hỏi: 21968
Hàm số f(x) có đạo hàm \(f'(x) = {x^2}{(x + 1)^2}\). Số cực trị của hàm số là
- A. 1
- B. 2
- C. 0
- D. 3
-
Câu 9: Mã câu hỏi: 21969
Hàm số f(x) có đạo hàm \(f'(x) = {x^2}{(x + 1)^2}(x + 2).\) Phát biểu nào sau đây là đúng:
- A. Hàm số đạt cực tiểu tại x = -2
- B. Hàm số đạt cực tiểu tại x = -2, x = 0. Hàm số đạt cực đại tại x = - 1
- C. Hàm số đạt cực đại tại x = -2, x = 0 Hàm số đạt cực tiểu tại x =-1
- D. Hàm số không có cực trị.
-
Câu 10: Mã câu hỏi: 21970
Giá trị cực đại của hàm số \(y = {x^3} - 3x + 2\) là:
- A. -1
- B. 1
- C. 0
- D. 4
-
Câu 11: Mã câu hỏi: 21973
Cho hàm số có bảng biến thiên dưới đây. Phát biểu nào là đúng?
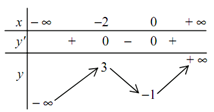
- A. Hàm số đạt cực tiểu tại x = -1 và đạt cực đại tại x = 3
- B. Giá trị cực tiểu của hàm số là 0
- C. Giá trị cực đại của hàm số là -2
- D. Hàm số đạt cực đại tại x = -2 và đạt cực tiểu tại x = 0
-
Câu 12: Mã câu hỏi: 21975
Điểm cực đại của đồ thị hàm số \(y = \frac{1}{2}{x^4} - 2{x^2} - 3\) là:
- A. (0;-3)
- B. 0
- C. \((\sqrt{-2};-5);(\sqrt{2};-5)\)
- D. -3
-
Câu 13: Mã câu hỏi: 21978
Cho hàm số có bảng biến thiên sau
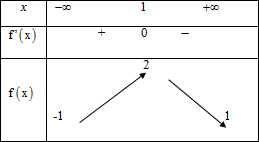
Trong các khẳng định sau khẳng định nào đúng?- A. Đồ thị hàm số có hai tiệm cận ngang là y=-1, y=1
- B. Đồ thị hàm số có hai tiệm cận ngang là x=-1,x=1
- C. Đồ thị hàm số không có tiệm cận ngang.
- D. Đồ thị hàm số có có tiệm cận đứng.
-
Câu 14: Mã câu hỏi: 21980
Cho hàm số \(y = \frac{{x + 1}}{{\sqrt {{x^2} - 1} }}.\) Số tiệm cận ngang của đồ thị hàm số là:
- A. 1
- B. 2
- C. 0
- D. Không thể xác định được
-
Câu 15: Mã câu hỏi: 21982
Cho hàm số \(y = \frac{{2x - 3}}{{x + 1}}\). Giao điểm hai đường tiệm cận của đồ thị hàm số có tọa độ là:
- A. (-1;2)
- B. \((\frac{3}{2};2)\)
- C. (2; -1)
- D. \((-1;\frac{3}{2})\)
-
Câu 16: Mã câu hỏi: 21985
Cho hàm số \(y = {x^3} + 5x + 7.\) Giá trị lớn nhất của hàm số trên đoạn [-5; 0] là:
- A. 7
- B. -143
- C. 6
- D. 8
-
Câu 17: Mã câu hỏi: 21987
Cho hàm số có bảng biến thiên sau
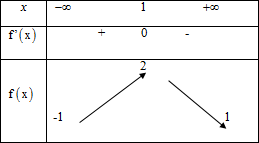
Trong các khẳng định sau khẳng định nào đúng?- A. Giá trị lớn nhất của hàm số là 2.
- B. Giá trị nhỏ nhất của hàm số là -1
- C. Giá trị nhỏ nhất của hàm số là -1 và 1
- D. Giá trị lớn nhất của hàm số là 1
-
Câu 18: Mã câu hỏi: 21988
Giá trị nhỏ nhất của hàm số \(y = \sin x - \frac{4}{3}{\sin ^3}x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) bằng:
- A. \(-\frac{1}{3}\)
- B. 1
- C. \(\frac{1}{3}\)
- D. -3
-
Câu 19: Mã câu hỏi: 21989
Cho biểu thức \(A = \frac{{2xy}}{{{x^2} + {y^2}}},\) với \(x, y\neq 0\) Giá trị nhỏ nhất của A bằng:
- A. 1
- B. 0
- C. -1
- D. Không có giá trị nhỏ nhất
-
Câu 20: Mã câu hỏi: 21990
Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật, đáy là hình vuông và thể tích khối hộp được tạo thành là 8 dm3 Độ dài cạnh đáy của mỗi hộp muốn thiết kế để diện tích toàn phần đạt giá trị nhỏ nhất là:
- A. \(2\sqrt[3]{2}\)
- B. 2
- C. 4
- D. Không có giá trị nhỏ nhất






