Phương pháp giải bài toán liên quan đến hai vật môn Vật Lý 12 năm 2021-2022

Ta khảo sát các bài toán sau:

+ Các vật cùng dao động theo phương ngang.

+ Các vật cùng dao động theo phương thắng đứng.

1.1. Hai vật tách rời ở vị trí cân bằng 

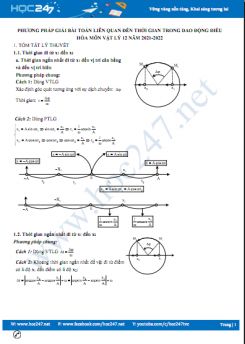
+ Giai đoạn 1: Cả hai vật cùng dao động với biên độ A, tần số góc \(\omega =\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}\)  và tốc độ cực đại \({{v}_{0}}=\omega A.\)

+ Giai đoạn 2: Nếu đến VTCB m₂ tách ra khỏi m₁ thì

* m₁ dao đông điều hòa với tần số góc \(\omega =\sqrt{\frac{k}{m}}\) và biên độ \(A'=\frac{{{v}_{0}}}{\omega '}=A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}\) (vì tốc độ cực đại không đổi vẫn là v₀!).

* m₂ chuyển động thẳng đều với vận tốc v₀ và khi m₁ đến vị trí biên dương (lần 1) thì

m₂ đi đươc quãng đường \(S={{v}_{0}}\frac{T'}{4}=\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}.A.\frac{1}{4}2\pi \sqrt{\frac{{{m}_{1}}}{k}}=\frac{\pi }{2}A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}\)

Lúc này khoảng cách hai vật: \(\Delta x=S-A'=A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}\left( \frac{\pi }{2}-1 \right)\)

1.2. Cắt bớt vật (đặt thêm vật)

Cất bớt vật (đặt thêm vật) lúc tốc độ dao động cực đại sao cho không làm thay đổi biên độ \(A'=A\Rightarrow \frac{v_{\max }^{'}}{{{v}_{\max }}}=\frac{\omega 'A'}{\omega A}=\frac{\sqrt{\frac{k}{m}}}{\sqrt{\frac{k}{m+\Delta m}}}=\sqrt{\frac{m+\Delta m}{m}}\)

+ Cất bớt vật (đặt thêm vật) lúc tốc độ dao động cực đại sao cho không làm thay đổi tốc độc cực đại : \(v_{\max }^{'}={{v}_{\max }}\Rightarrow \frac{A'}{A}=\frac{\frac{v_{\max }^{'}}{\omega '}}{\frac{{{v}_{\max }}}{\omega }}=\frac{\sqrt{\frac{k}{m+\Delta m}}}{\sqrt{\frac{k}{m}}}=\sqrt{\frac{m}{m+\Delta m}}\)

+ Cất bớt vật (đặt thêm vật) lúc hệ có li độ x₁ (vận tốc x₁) sao cho không làm thay đổi vận tốc tức thời:

Ngay trước lúc tác động: \({{A}^{2}}=x_{1}^{2}+\frac{v_{1}^{2}}{{{\omega }^{2}}}=x_{1}^{2}+v_{1}^{2}\frac{m+\Delta m}{k}\Rightarrow v_{1}^{2}=\frac{k}{m+\Delta m}\left( {{A}^{2}}-{{x}^{2}} \right)\)

Ngay sau lúc tác động:

\(A'=\sqrt{x_{1}^{2}+\frac{v_{1}^{2}}{{{\omega }^{'2}}}}=\sqrt{x_{1}^{2}+\frac{k}{m+\Delta m}\left( {{A}^{2}}-x_{1}^{2} \right)\frac{m}{k}}=\sqrt{x_{1}^{2}+\left( {{A}^{2}}-x_{1}^{2} \right)\frac{m}{m+\Delta m}}\)

1.3. Liên kết giữa hai vật

+ Để hai vật cùng dao động thì lực liên kết không nhỏ hơn lực quán tính cực đại tác dụng lên m₂: \){{F}_{lk}}\ge {{F}_{qt\max }}={{m}_{2}}{{\omega }^{2}}A={{m}_{2}}\frac{k}{{{m}_{1}}+{{m}_{2}}}A\)

Ví dụ 1: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ m₁. Ban đầu giữ vật m₁ tại vị trí mà lò xo bị nén 8 cm, đặt vật nhỏ m₂ (có khối lượng bằng khối lượng vật  m₁ trên mặt phẳng nằm ngang và sát với vật m₁. Buông nhẹ để hai vật bắt đầu chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên thì khoảng cách giữa hai vật m₁ và m₂ là

A. 4,6 cm.                  

B. 2,3 cm.                   

C. 5,7 cm.                  

D. 3,2 cm.

Hướng dẫn

+ Giai đoan 1: Cả hai vât cùng dao đông với biên đô A, tần số góc \(\omega =\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}\) tốc độ cực đại \({{v}_{0}}=\omega A\) .

+ Giai đoạn 2: Đến VTCB m₂ tách khỏi m₁ thì:

* m₁ dao đông điều hòa với tần số góc \(\omega '=\sqrt{\frac{k}{{{m}_{1}}}}\) và biên độ \(A'=\frac{{{v}_{0}}}{\omega '}=A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}\)

(vì tốc độ cực đại không đổi vẫn là v₀!).

* m₂ chuyển động thẳng đều với vận tốc v₀ và khi m₁ đến vị trí biên dương (lần 1) thì m₂ đi được quãng đường \(S={{v}_{0}}\frac{T'}{4}=\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}A.\frac{1}{4}2\pi \sqrt{\frac{{{m}_{1}}}{k}}=\frac{\pi }{2}A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}\)

Lúc này khoảng cách giữa hai vật:

\(\Delta x=S-A'=\frac{\pi A}{2}\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}-A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}\approx 3,2\left( cm \right)\Rightarrow \) Chọn D.

Ví dụ 2: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có độ cứng 300N/m, một đầu cố định, đầu kia gắn với vật nhỏ M = 3kg. Vật M đang ở vị trí cân bằng thì vật nhỏ m = 1kg chuyển động với vận tốc v₀ = 2m/s đến va chạm mềm vào nó theo xu hướng làm cho lò xo nén. Biết rằng khi trở lại vị trí va chạm thì hai vật tự tách ra. Tổng độ nén cực đại của lò xo và độ dãn cực đại của lò xo là:

A. 10,8 cm.                

B. 11,6 cm                  

C. 5,0cm        

D. 10,0cm.

Hướng dẫn

Vân tốc của hê ngay sau va cham: \(V=\frac{m{{v}_{0}}}{m+M}\)= 0,5 (m/s) (đây chính là tốc độ cực đại của dao động điều hòa). Sau đó cả hai vật chuyển động về bên trái làm cho lò xo nén cực đại \(A=\frac{V}{\omega }=V\sqrt{\frac{M+m}{k}}=0,5\sqrt{\frac{3+1}{300}}\approx 0,058\left( m \right)=5,8\left( cm \right)\)

Rồi tiếp đó cả hai vật chuyển động về bên phải, đúng lúc về vị trí cân bằng thì vật m tách ra chỉ còn M dao động điều hòa với tốc độ cực đại vẫn là V và độ dãn cực đại của lò xo \(A'=\frac{V}{\omega '}=V\sqrt{\frac{M}{k}}=0,5\sqrt{\frac{3}{300}}-0,05\left( m \right)=5\left( cm \right)\)

Tổng độ nén cực đại và độ dãn cực đại của lò xo là 5,8 + 5 = 10,8 (cm) → Chọn A.

Ví dụ 3:  Một con lắc lò xo đặt trên mặt phang nằm ngang gồm lò xo nhẹ có độ cứng 300 N/m, một đầu cố định, đầu kia gắn với vật nhỏ M = 3 kg. Vật M đang ở vị trí cân bằng thì vật nhỏ m = 1 kg chuyển động với vận tốc v₀ = 2 m/s đến va chạm mềm vào nó theo xu hướng làm cho lò xo nén. Biết rằng, khi trở lại vị trí va chạm thì hai vật tự tách ra. Lúc lò xo có chiều dài cực đại lần đầu tiên thì khoảng cách M và m là 

A. 2,85 cm.                

B. 5,8 cm.                   

C. 7,85 cm.                

D. 10 cm.

Hướng dẫn

Vận tốc của hệ ngay sau va chạm: \(V=\frac{m{{v}_{0}}}{m+M}=0,5\left( m/s \right)\) đây chính là tốc độ cực đại của dao động điều hòa. Sau đó cả hai cùng chuyển động về bên phải rồi về been trái và đúng lúc trở về vị trí cân bằng với tốc độ V thì m tách ra tiếp theo thì:

* M dao động điều hòa với tần số \(\omega '=\sqrt{\frac{k}{M}}\) , biên độ \(A'=\frac{V}{\omega '}=V\sqrt{\frac{M}{k}}=0,05\left( m \right)\)

(vì tốc độ cực đại không đổi vẫn là V).

* m chuyển động thẳng đều với vận tốc V và khi M đến vị trí biên dưcmg (lần 1) thì m

đi đươc quãng đường \(S=V\frac{T'}{4}=V.\frac{1}{4}2\pi \sqrt{\frac{M}{k}}\approx 0,0785\left( m \right)\)

Lúc này khoảng cách giữa hai vật: \(\Delta S=S-A'=0,0285\left( m \right)\)

Chọn A.

Ví dụ 4: Con lắc lò xo nằng ngang gồm lò xo có độ cứng k = 100N/m gắn  với vật m₁ = 100g. Ban đầu vật m₁ được giữ tại vịt trí lò xo bị nén 4cm, đặt vật m₂ = 300g tại vị trí cân bằng O của vật m₁. Buông nhẹ m₁ để nó đến va chạm mềm với m₂, hạt vật dính vào nhau coi các vật là chất điểm, bỏ qua ma sát lấy π² = 10. Quãng đường vật m₁ đi được sau 121/60s kể từ khi buông m₁ là:

A. 40,58 cm.   

B. 42,58 cm.     

C. 38,58 cm.    

D. 43,00 cm.

Hướng dẫn

Từ M đến O chỉ mình m₁ dao động điều hòa với biên độ A = 4cm và chu kỳ \({{T}_{1}}=2\pi \sqrt{\frac{{{m}_{1}}}{k}}=0,2\left( s \right)\) . Đúng lúc đến O tốc độ của m₁ là \({{v}_{\max }}=\omega A\) ngày sau va chạm hai vật dính vào nhau và có cùng tốc độ: v'_max =  \(\frac{{{m}_{1}}{{v}_{\max }}}{{{m}_{1}}+{{m}_{2}}}\) và đây cũng chính là tốc độ cực đại của dao động điều hòa của cả hai vật, biên độ dao động mới 

\(A'=\frac{v_{\max }^{'}}{\omega '}=\frac{\frac{{{m}_{1}}\omega A}{{{m}_{1}}+{{m}_{2}}}}{\omega '}=A\sqrt{\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}}=2\left( cm \right)\)

Và chu kỳ dao động mới: \({{T}_{2}}=2\pi \sqrt{\frac{{{m}_{1}}+{{m}_{2}}}{k}}=0,4\left( s \right)\)

Ta phân tích thời gian: \(t=\frac{121}{60}s=0,05+1,9+\frac{1}{15}++19+\)

\(\Rightarrow S=A+19A'+0,5A'=43,00\left( cm \right)\Rightarrow \) Chọn D.

--- (Toàn bộ nội dung, chi tiết phần ví dụ minh họa tài liệu các em vui lòng xem Online hoặc Đăng nhập vào HOC247 đề tải về máy) ---

Bài 1 : Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ m₁ . Ban đầu giữ vật m₁ tại vị trí mà lò xo bị nén 8 cm, đặt vật nhỏ m₂ (có khối lượng bằng khối lượng vật m₁ ) trên mặt phẳng nằm ngang và sát với vật m₁ . Buông nhẹ để hai vật bắt đầu chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Độ dãn cực đại của lò xo là

A. 4,6 cm.                  

B. 2,3 cm.                   

C. 5,7 cm.                  

D. 3,2 cm.

Bài 2: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ m₁. Giữ vật m₁ tại vị trí mà lò xo bị nén 8 cm, đặt vật nhỏ m₂ (có khối lượng bằng lchối lượng vật m₁ ) trên mặt phẳng nằm ngang và sát với vật m₁. Ở thời điểm t = 0, buông nhẹ để hai vật bắt đầu chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. ở thời điểm lò xo có chiều dài cực đại lần đầu tiên thì m₂ đi được một đoạn là

A. 4,6 cm.                  

B. 16,9 cm.                 

C. 5,7 cm.                  

D. 16 cm.

Bài 3: Một vật có khối lượng m = 100 g được mắc vào 1 lò xo nhẹ có k = 100 N/m, đầu kia được nối với tường. Bỏ qua ma sát trong quá trình chuyển động. Đặt vật thứ 2 có khối lượng m’ = 300 g sát vật m và đưa hệ về vị trí lò xo nén 4 cm sau đó buông nhẹ. Tính khoảng cách giữa hai vật khi hai vật chuyển động ngược chiều nhau lần đầu tiên

A. 10,28 cm.              

B. 5,14 cm.                 

C. 1,14 cm.                

D. 2,28 cm.

Bài 4: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có độ cứng 300 N/m, một đầu cố định, đầu kia gắn với vật nhỏ M = 3 kg. Vật M đang ở vị trí cân bằng thì vật nhỏ m = 1 kg chuyển động với vận tốc v₀ = 2 m/s đến va chạm mềm vào nó theo xu hướng làm cho lò xo nén. Biết rằng, khi trở lại vị trí va chạm thì hai vật tự tách ra. Độ dãn cực đại của lò xo là

A. 2,85 cm.                

B. 16,90 cm.               

C. 5,00 cm.                

D. 6,00 cm.

Bài 5: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có độ cứng 400 N/m, một đầu cố định, đầu kia gắn với vật nhỏ M = 4 kg. Vật M đang ở vị trí cân bằng thì vật nhỏ m = 1 kg chuyển động với vận tốc v₀ = 2 m/s đến va chạm mềm vào nó theo xu hướng làm cho lò xo nén. Biết rằng, khi trở lại vị trí va chạm thì hai vật tự tách ra. Độ dãn cực đại của lò xo là

A. 2,85 cm.                

B. 4,00 cm.                 

C. 5,00 cm.                

D. 6,00 cm.

Bài 6: Con lắc lò xo nằm ngang gồm lò xo có độ cứng k = 100 N/m gắn với vật m₁ = 100 g. Ban đầu vật m₁ được giữ tại vị trí lò xo bị nén 4 cm, đặt vật m₂ = 300 g tại vị trí cân bằng O của m₁. Buông nhẹ m₁ để nó đến va chạm mềm với m₂, hai vật dính vào nhau, coi các vật là chất điểm, bỏ qua mọi ma sát, lấy π² = 10. Quãng đường vật m₁ đi được sau 1,95 s kể từ khi buông m₁ là

A. 40,58 cm.              

B. 42,58 cm.               

C. 38,58 cm.              

D. 42,00 cm.

Bài 7: Con lắc lò xo nằm ngang gồm lò xo có độ cứng k = 100 N/m gắn với vật m₁ = 100 g. Ban đầu vật m₁ được giữ tại vị trí lò xo bị nén 4 cm, đặt vật m₂ = 300 g tại vị trí cân bằng O của m₁. Buông nhẹ m₁ để nó đến va chạm mềm với m₂, hai vật dính vào nhau, coi các vật là chất điểm, bỏ qua mọi ma sát, lấy π² = 10. Quãng đường vật m₁ đi được sau 2 s kể từ khi buông m₁ là

A. 40,58 cm.              

B. 42,58 cm.               

C. 38,58 cm.              

D. 36,58 cm.

Bài 8: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có độ cứng 300 N/m, một đầu cố định, đầu kia gắn với vật nhỏ M = 3 kg. Vật M đang ở VTCB thì vật nhỏ m = 1 kg chuyển động với vận tốc v₀ = 2 m/s đến va chạm vào nó theo xu hướng làm cho lò xo nén. Lúc lò xo có chiều dài cực đại lần đầu tiên thì khoảng cách M và m là bao nhiêu? Xét trường hợp va chạm đàn hồi.

A. 2,85 cm.                

B. 16,9 cm.                 

C. 37 cm.                   

D. 16 cm.

Bài 9: Một con lắc lò xo gồm lò xo có độ cứng k và vật có khối lượng m₁ , dao động điều hòa trên mặt ngang. Khi li độ m₁ là 2,5 cm thì vận tốc của nó là \(25\sqrt{3}\) cm/s. Khi li độ là 2,5\(\sqrt{3}\) cm thì vận tốc là 25 cm/s. Đúng lúc m₁ qua vị trí cân bằng thì vật m₂ cùng khối lượng chuyển động ngược chiều với vận tốc 1 m/s đến va chạm đàn hồi xuyên tâm với m₁ . Chọn gốc thời gian là lúc va chạm, vào thời điểm mà tốc độ của m₁ bằng \(\sqrt{3}\) lần tốc độ của m₂ lần thứ nhất thì hai vật cách nhau bao nhiêu?

A. 13,9 cm.                

B. 7,6 cm.                   

C. 10\(\sqrt{3}\) cm.              

D. 5\(\sqrt{3}\) cm.

Bài 10: Một con lắc lò xo gồm lò xo và quả cầu nhỏ m dao động điều hòa trên mặt ngang với biên độ 5 cm và tần số góc 10 rad/s. Đúng lúc quả cầu qua vị trí cân bằng thì một quả cầu nhỏ cùng khối lượng chuyển động ngược chiều với vận tốc 1 m/s đến va chạm đàn hồi xuyên tâm với quả cầu con lắc. Vào thời điểm mà vận tốc của m bằng 0 lần thứ hai thì hai quả cầu cách nhau bao nhiêu?

A. 13,9 cm.                

B. 17,85 cm.               

C. 33,6 cm.                

D. 13,6 cm.

ĐÁP ÁN PHẦN LUYỆN TẬP

1.C

2.B

3.C

4.C

5.B

6.D

7.B

8.C

9.B

10.D

 

Trên đây là một đoạn trích dẫn nội dung Phương pháp giải bài toán liên quan đến hai vật môn Vật Lý 12 năm 2021-2022. Để xem thêm nhiều tài liệu tham khảo hữu ích khác của các chức năng chọn xem trực tuyến hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học tập tốt và đạt được thành tích cao trong học tập!