C├╣ng Hß╗īC247 tham khß║Żo nß╗Öi dung t├Āi liß╗ću Ph├│ng xß║Ī v├Ā c├Īc dß║Īng b├Āi tß║Łp vß╗ü ph├│ng xß║Ī m├┤n Vß║Łt L├Į 12 n─ām 2021-2022 do ban bi├¬n tß║Łp Hß╗īC247 tß╗Ģng hß╗Żp v├Ā bi├¬n soß║Īn nhß║▒m gi├║p c├Īc em sß║Į h├¼nh dung ─æŲ░ß╗Żc c├Īc kiß║┐n thß╗®c trß╗Źng t├óm ─æß╗ā c├│ thß╗ā ├┤n tß║Łp thß║Łt tß╗æt. Mß╗Øi c├Īc em c├╣ng tham khß║Żo!
1. T├ōM Tß║«T L├Ø THUYß║ŠT
1.1. Kh├Īi niß╗ćm
Ph├│ng xß║Ī l├Ā hiß╗ćn tŲ░ß╗Żng hß║Īt nh├ón kh├┤ng bß╗ün tß╗▒ ─æß╗Öng ph├│ng ra c├Īc tia ph├│ng xß║Ī (c├Īc hß║Īt + s├│ng ─æiß╗ćn tß╗½) v├Ā biß║┐n th├Ānh hß║Īt nh├ón kh├Īc. V├Ł dß╗ź: \({}_{92}^{235}U\to \alpha +_{90}^{231}Th\)
NgŲ░ß╗Øi ta quy Ų░ß╗øc, gß╗Źi hß║Īt nh├ón ph├│ng xß║Ī l├Ā hß║Īt nh├ón mß║╣ v├Ā hß║Īt nh├ón sß║Żn phß║®m ph├ón r├Ż l├Ā hß║Īt nh├ón con.
1.2. ─Éß║Ęc ─æiß╗ām
+) Ph├│ng xß║Ī c├│ bß║Żn chß║źt l├Ā mß╗Öt phß║Żn ß╗®ng hß║Īt nh├ón.
+) Qu├Ī tr├¼nh ph├ón r├Ż ph├│ng xß║Ī chß╗ē do c├Īc nguy├¬n nh├ón b├¬n trong g├óy ra v├Ā ho├Ān to├Ān kh├┤ng chß╗ŗu t├Īc ─æß╗Öng cß╗¦a c├Īc yß║┐u tß╗æ thuß╗Öc m├┤i trŲ░ß╗Øng ngo├Āi nhŲ░ nhiß╗ćt ─æß╗Ö ├Īp suß║źt,...
+) L├Ā qu├Ī tr├¼nh tß╗▒ ph├Īt, ngß║½u nhi├¬n v├Ā kh├┤ng ─æiß╗üu khiß╗ān ─æŲ░ß╗Żc.
1.3. C├Īc tia ph├│ng xß║Ī
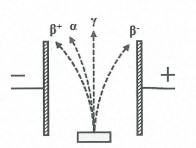
C├│ 3 loß║Īi tia ph├│ng xß║Ī: \(\alpha ,\beta ,\gamma \) kh├┤ng nh├¼n thß║źy ─æŲ░ß╗Żc nhŲ░ng c├│ nhß╗»ng ─æß║Ęc ─æiß╗ām m├Ā gi├║p ta c├│ thß╗ā ph├Īt hiß╗ćn ra, nhŲ░ k├Łch th├Łch mß╗Öt sß╗æ phß║Żn ß╗®ng h├│a hß╗Źc, ion h├│a kh├┤ng kh├Ł, l├Ām ─æen k├Łnh ß║Żnh,...
a) Tia anpha (╬▒)
- Tia \(\alpha \)c├│ bß║Żn chß║źt l├Ā ch├╣m hß║Īt nh├ón \({}_{2}^{4}He\) mang ─æiß╗ćn t├Łch dŲ░ŲĪng n├¬n bß╗ŗ lß╗ćch vß╗ü ph├Ła bß║Żn tß╗ź ├óm khi bay v├Āo ─æiß╗ćn trŲ░ß╗Øng giß╗»a hai bß║Żn cß╗¦a tß╗ź ─æiß╗ćn.
PhŲ░ŲĪng tr├¼nh ph├│ng xß║Ī: \({}_{Z}^{A}X\xrightarrow{{}}\,{}_{Z-2}^{A-4}\,Y+{}_{2}^{4}\,\alpha \)
So vß╗øi hß║Īt nh├ón mß║╣, hß║Īt nh├ón con l├╣i 2 ├┤ trong bß║Żng HTTH v├Ā c├│ sß╗æ khß╗æi nhß╗Å hŲĪn 4 ─æŲĪn vß╗ŗ.
- C├Īc t├Łnh chß║źt tia \(\alpha \):
+) Ph├│ng ra vß╗øi vß║Łn tß╗æc khoß║Żng \({{2.10}^{7}}{m}/{s}\;,\) l├Ām ion h├│a m├┤i trŲ░ß╗Øng v├Ā mß║źt dß║¦n n─āng lŲ░ß╗Żng.
+) Khß║Ż n─āng ─æ├óm xuy├¬n yß║┐u, ─æi ─æŲ░ß╗Żc chß╗½ng v├Āi cm trong kh├┤ng kh├Ł, kh├┤ng xuy├¬n qua ─æŲ░ß╗Żc tß║źm thß╗¦y tinh mß╗Ång.
b) Tia bêta (β).
- Tia \(\beta \) gß╗ōm 2 loß║Īi:
+) Tia \({{\beta }^{-}}\) c├│ bß║Żn chß║źt l├Ā ch├╣m ├¬lectr├┤n \(\left( _{-1}^{0}e \right)\) mang ─æiß╗ćn t├Łch ├óm n├¬n lß╗ćch vß╗ü ph├Ła bß║Żn tß╗ź dŲ░ŲĪng khi bay trong ─æiß╗ćn trŲ░ß╗Øng giß╗»a hai bß║Żn tß╗ź.
PhŲ░ŲĪng tr├¼nh ph├│ng xß║Ī \({{\beta }^{-}}:\,\,_{Z}^{A}X\to _{Z+1}^{A}Y+_{-1}^{0}e+_{0}^{0}\overline{v}\)
\(\overline{v}\) l├Ā phß║Żn nŲĪtrin├┤, kh├┤ng mang ─æiß╗ćn, c├│ sß╗æ khß╗æi A = 0, chuyß╗ān ─æß╗Öng vß╗øi vß║Łn tß╗æc ├Īnh s├Īng.
So vß╗øi hß║Īt nh├ón mß║╣ X, hß║Īt nh├ón con Y tiß║┐n 1 ├┤ trong bß║Żng HTTH v├Ā c├│ c├╣ng sß╗æ khß╗æi.
+) Tia \({{\beta }^{+}}\)c├│ bß║Żn chß║źt l├Ā ch├╣m hß║Īt c├│ khß╗æi lŲ░ß╗Żng nhŲ░ electr├┤n nhŲ░ng mang ─æiß╗ćn t├Łch (+e), gß╗Źi l├Ā c├Īc p├┤zitr├┤n \(\left( _{1}^{0}e \right)\) v├Ā lß╗ćch vß╗ü ph├Ła bß║Żn tß╗ź ├óm khi bay v├Āo trong ─æiß╗ćn trŲ░ß╗Øng giß╗»a hai bß║Żn tß╗ź ─æiß╗ćn.
PhŲ░ŲĪng tr├¼nh ph├│ng xß║Ī \({{\beta }^{+}}:\,\,_{Z}^{A}X\to _{Z-1}^{A}Y+_{1}^{0}e+_{0}^{0}\overline{v}\)
So vß╗øi hß║Īt nh├ón mß║╣ X, hß║Īt nh├ón con Y l├╣i 1 ├┤ trong bß║Żng HTTH v├Ā c├│ c├╣ng sß╗æ khß╗æi.
- C├Īc t├Łnh chß║źt cß╗¦a tia \(\beta \):
+) Ph├│ng ra vß╗øi vß║Łn tß╗æc gß║¦n bß║▒ng vß║Łn tß╗æc ├Īnh s├Īng.
+) L├Ām ion h├│a m├┤i trŲ░ß╗Øng nhŲ░ng yß║┐u hŲĪn tia \(\alpha \).
+) Khß║Ż n─āng ─æ├óm xuy├¬n mß║Īnh hŲĪn tia \(\alpha \), ─æi ─æŲ░ß╗Żc v├Āi m├®t trong kh├┤ng kh├Ł v├Ā v├Āi mm trong kim loß║Īi.
c) Tia gamma (╬│)
- Tia \(\gamma \) c├│ bß║Żn chß║źt s├│ng ─æiß╗ćn tß╗½ c├│ bŲ░ß╗øc s├│ng rß║źt ngß║»n.
Ph├│ng xß║Ī \(\gamma \) kh├┤ng c├│ sß╗▒ biß║┐n ─æß╗Ģi hß║Īt nh├ón, chß╗ē c├│ sß╗▒ chuyß╗ān trß║Īng th├Īi v├Ā ph├Īt bß╗®c xß║Ī: \(hf={{E}_{2}}-{{E}_{1}}.\)
- C├Īc t├Łnh chß║źt cß╗¦a tia \(\gamma :\)
+) Mang n─āng lŲ░ß╗Żng lß╗øn.
+) C├│ khß║Ż n─āng ─æ├óm xuy├¬n rß║źt mß║Īnh, c├│ thß╗ā ─æi qua lß╗øp ch├¼ h├Āng chß╗źc cm, g├óy nguy hiß╗ām ─æß╗æi vß╗øi cŲĪ thß╗ā con ngŲ░ß╗Øi.
+) Bß╗®c xß║Ī \(\gamma \) lu├┤n ─æi k├©m theo sau sß╗▒ ph├│ng xß║Ī \(\alpha \) hoß║Ęc \(\beta .\)
1.4. ─Éß╗ŗnh luß║Łt ph├│ng xß║Ī
a) Chu kß╗│ b├Īn r├Ż (T).
Mß╗Śi mß║½u chß║źt ph├│ng xß║Ī ─æŲ░ß╗Żc ─æß║Ęc trŲ░ng bß╗¤i mß╗Öt thß╗Øi gian T gß╗Źi l├Ā chu kß╗│ b├Īn r├Ż, l├Ā khoß║Żng thß╗Øi gian m├Ā mß╗Öt nß╗Ła lŲ░ß╗Żng chß║źt ph├│ng xß║Ī bß╗ŗ ph├ón r├Ż th├Ānh hß║Īt nh├ón nguy├¬n tß╗Ł kh├Īc.
b) ─Éß╗ŗnh luß║Łt ph├│ng xß║Ī.
- X├®t mß╗Öt mß║½u ph├│ng xß║Ī.
+) \({{N}_{o}}\) l├Ā sß╗æ hß║Īt nh├ón ban ─æß║¦u cß╗¦a mß║½u.
+) N l├Ā sß╗æ hß║Īt nh├ón c├▓n lß║Īi sau thß╗Øi gian t l├Ā: \(N={{N}_{o}}{{.2}^{\frac{-t}{T}}}={{N}_{o}}.{{e}^{-\lambda t}}.\)
Vß╗øi \(\lambda =\frac{\ln 2}{T}\left( {{s}^{-1}} \right)\) gß╗Źi l├Ā hß║▒ng sß╗æ ph├│ng xß║Ī, ─æß║Ęc trŲ░ng cho tß╗½ng chß║źt ph├│ng xß║Ī.

Sß╗æ hß║Īt nh├ón ph├│ng xß║Ī giß║Żm theo quy luß║Łt h├Ām sß╗æ m┼®
c) Hoß║Īt ─æß╗Ö ph├│ng xß║Ī (H)
- L├Ā ─æß║Īi lŲ░ß╗Żng ─æß║Ęc trŲ░ng cho t├Łnh ph├│ng xß║Ī mß║Īnh hay yß║┐u cß╗¦a mß╗Öt lŲ░ß╗Żng chß║źt ph├│ng xß║Ī, ─æŲ░ß╗Żc ─æo bß║▒ng sß╗æ ph├ón r├Ż trong 1 gi├óy. K├Ł hiß╗ću: H, ─æŲĪn vß╗ŗ BecŲĪren (Bq) hoß║Ęc Curi (Ci)
1 gi├óy r├Ż/gi├óy = 1 Bq; \(1Ci=3,{{7.10}^{10}}Bq.\)
- ─Éß╗Ö ph├│ng xß║Ī H giß║Żm theo thß╗Øi gian vß╗øi quy luß║Łt: \({{H}_{\left( t \right)}}=-\frac{\Delta N}{\Delta t}=\lambda .{{N}_{o}}.{{e}^{-\lambda t}}=\lambda {{N}_{\left( t \right)}}\)
\(\Rightarrow \left\{ \begin{align} & {{H}_{o}}=\lambda {{N}_{o}} \\ & {{H}_{\left( t \right)}}=\lambda {{N}_{\left( t \right)}} \\ \end{align} \right.\)\(\Rightarrow {{H}_{\left( t \right)}}={{H}_{o}}{{.2}^{-\frac{t}{T}}}={{H}_{o}}.{{e}^{-\lambda t}},\)
Vß╗øi \({{H}_{o}}\) l├Ā ─æß╗Ö ph├│ng xß║Ī ban ─æß║¦u.
2. Mß╗śT Sß╗É Dß║ĀNG B├ĆI Tß║¼P
2.1. Dß║ĀNG 1: B├ĆI TO├üN ├üP Dß╗żNG ─Éß╗ŖNH LUß║¼T PH├ōNG Xß║Ā.
X├®t mß╗Öt mß║½u ph├│ng xß║Ī: \(X\to Y+\)tia ph├│ng xß║Ī.
Gß╗Źi \({{N}_{o}},{{m}_{o}}\) lß║¦n lŲ░ß╗Żt l├Ā sß╗æ hß║Īt nh├ón v├Ā khß╗æi lŲ░ß╗Żng cß╗¦a mß║½u ban ─æß║¦u.
- Sß╗æ hß║Īt nh├ón v├Ā khß╗æi lŲ░ß╗Żng ph├│ng xß║Ī c├▓n lß║Īi:
\(\left\{ \begin{align} & N={{N}_{o}}{{.2}^{\frac{-t}{T}}}={{N}_{o}}.{{e}^{-\lambda t}} \\ & m={{m}_{o}}{{.2}^{\frac{-t}{T}}}={{m}_{o}}.{{e}^{-\lambda t}} \\ \end{align} \right.\)
Trong ─æ├│: N, m lß║¦n lŲ░ß╗Żt l├Ā sß╗æ hß║Īt nh├ón, khß╗æi lŲ░ß╗Żng cß╗¦a mß║½u ph├│ng xß║Ī c├▓n lß║Īi sau thß╗Øi gian t.
- Sß╗æ hß║Īt nh├ón v├Ā khß╗æi lŲ░ß╗Żng ph├│ng xß║Ī ─æ├Ż bß╗ŗ ph├ón r├Ż:
\(\left\{ \begin{align} & \Delta N={{N}_{o}}-N={{N}_{o}}\left( 1-{{2}^{\frac{-t}{T}}} \right)={{N}_{o}}(1-{{e}^{-\lambda t}}) \\ & \Delta m={{m}_{o}}-m={{m}_{o}}\left( 1-{{2}^{\frac{-t}{T}}} \right)={{m}_{o}}{{e}^{-\lambda t}} \\ \end{align} \right.\)
Trong ─æ├│: \(\Delta N,\,\,\Delta m\) lß║¦n lŲ░ß╗Żt l├Ā sß╗æ hß║Īt nh├ón, khß╗æi lŲ░ß╗Żng cß╗¦a mß║½u ─æ├Ż bß╗ŗ ph├ón r├Ż.
- Phß║¦n tr─ām sß╗æ hß║Īt, khß╗æi lŲ░ß╗Żng ph├│ng xß║Ī c├▓n lß║Īi: \(\frac{N}{{{N}_{o}}}=\frac{m}{{{m}_{o}}}=\frac{H}{{{H}_{o}}}={{2}^{\frac{-t}{T}}}={{e}^{-\lambda t}}\)
- Phß║¦n tr─ām sß╗æ hß║Īt, khß╗æi lŲ░ß╗Żng ph├│ng xß║Ī bß╗ŗ ph├ón r├Ż: \(\frac{\Delta N}{{{N}_{o}}}=\frac{\vartriangle m}{{{m}_{o}}}=1-{{2}^{\frac{-t}{T}}}=1-{{e}^{-\lambda t}}\)
Ch├║ ├Į: Mß╗æi li├¬n hß╗ć vß╗ü sß╗æ hß║Īt v├Ā khß╗æi lŲ░ß╗Żng: \(N=n.{{N}_{A}}=\frac{m}{A}.{{N}_{A}}\)
Trong ─æ├│: n l├Ā sß╗æ mol, \({{N}_{A}}=6,{{02.10}^{23}}mo{{l}^{-1}}\) l├Ā sß╗æ Av├┤ga─ær├┤.
V├Ł dß╗ź minh hß╗Źa: Chß║źt ph├│ng xß║Ī P├┤l├┤ni \(_{84}^{210}Po\) ph├│ng xß║Ī tia \(\alpha \)v├Ā biß║┐n th├Ānh hß║Īt nh├ón ch├¼ Pb. Biß║┐t chu kß╗│ b├Īn r├Ż cß╗¦a \(_{84}^{210}Po\) l├Ā 138 ng├Āy v├Ā ban ─æß║¦u c├│ 100g \(_{84}^{210}Po\). Lß║źy khß╗æi lŲ░ß╗Żng nguy├¬n tß╗Ł xß║źp xß╗ē sß╗æ khß╗æi A(u).
a) T├Łnh sß╗æ hß║Īt Po v├Ā khß╗æi lŲ░ß╗Żng Po c├▓n lß║Īi sau 69 ng├Āy?
b) T├Łnh sß╗æ hß║Īt Po bß╗ŗ ph├ón r├Ż v├Ā khß╗æi lŲ░ß╗Żng Po ─æ├Ż ph├ón r├Ż sau 80 ng├Āy?
c) Sau 150 ng├Āy c├│ bao nhi├¬u phß║¦n tr─ām Po bß╗ŗ ph├ón r├Ż?
d) Sau bao l├óu Po bß╗ŗ ph├ón r├Ż 12,5 g?
e) Sau bao l├óu (kß╗ā tß╗½ thß╗Øi ─æiß╗ām ban ─æß║¦u) sß╗æ hß║Īt nh├ón cß╗¦a \(_{84}^{210}Po\)ph├│ng xß║Ī c├▓n lß║Īi bß║▒ng 25% sß╗æ hß║Īt nh├ón ban ─æß║¦u?
Lß╗Øi giß║Żi
PhŲ░ŲĪng tr├¼nh phß║Żn ß╗®ng: \(_{84}^{210}Po\to _{2}^{4}\alpha +_{82}^{206}Pb.\)
Sß╗æ hß║Īt nh├ón Po ban ─æß║¦u c├│ trong mß║½u l├Ā
\({{N}_{o}}=\frac{m}{A}.{{N}_{A}}=\frac{100}{210}.6,{{02.10}^{23}}\approx 2,{{866.10}^{23}}\) hß║Īt.
a) Sau 69 ng├Āy, sß╗æ hß║Īt v├Ā khß╗æi lŲ░ß╗Żng Po c├▓n lß║Īi l├Ā
\(\left\{ \begin{align}
& {{N}_{\left( t \right)}}={{N}_{o}}{{.2}^{\frac{-t}{T}}}=2,{{866.10}^{23}}{{.2}^{\frac{-69}{138}}}=2,{{027.10}^{23}}hat \\
& {{m}_{\left( t \right)}}={{m}_{o}}{{.2}^{\frac{-t}{T}}}={{100.2}^{\frac{-69}{138}}}=50\sqrt{2}g \\
\end{align} \right.\)
b) Sau 80 ng├Āy, sß╗æ hß║Īt Po ─æ├Ż bß╗ŗ ph├ón r├Ż l├Ā
\(\Delta N={{N}_{o}}\left( 1-{{2}^{-\frac{t}{T}}} \right)=2,{{866.10}^{23}}.\left( 1-{{2}^{\frac{-80}{138}}} \right)=9,{{48.10}^{22}}\) hß║Īt.
Sau 80 ng├Āy, khß╗æi lŲ░ß╗Żng Po ─æ├Ż bß╗ŗ ph├ón r├Ż l├Ā:
\(\Delta m={{m}_{o}}\left( 1-{{2}^{-\frac{t}{T}}} \right)=100\left( 1-{{2}^{-\frac{80}{138}}} \right)\approx 33,1g.\)
c) Sau 150 ng├Āy, phß║¦n tr─ām Po bß╗ŗ ph├ón r├Ż l├Ā
\(\frac{\Delta m}{m}=1-{{2}^{-\frac{t}{T}}}=1-{{2}^{-\frac{150}{380}}}=52,924%.\)
d) Khß╗æi lŲ░ß╗Żng Po ─æ├Ż bß╗ŗ ph├ón ra:
\(\Delta m={{m}_{o}}\left( 1-{{2}^{-\frac{t}{T}}} \right)\Leftrightarrow 12,5=100\left( 1-{{2}^{\frac{-t}{138}}} \right)\Rightarrow t\approx 26,6\) ng├Āy.
e) Sß╗æ hß║Īt nh├ón Po ph├│ng xß║Ī c├▓n lß║Īi 25% so vß╗øi ban ─æß║¦u:
\(\frac{N}{{{N}_{o}}}={{2}^{-\frac{t}{T}}}\Leftrightarrow 0,25={{2}^{\frac{-t}{138}}}\Rightarrow t=276\) ng├Āy.
2.2. Dß║ĀNG 2: B├ĆI TO├üN Sß╗É Hß║ĀT NH├éN V├Ć KHß╗ÉI LŲ»ß╗óNG Hß║ĀT NH├éN CON Tß║ĀO TH├ĆNH.
- Sß╗æ hß║Īt nh├ón v├Ā khß╗æi lŲ░ß╗Żng cß╗¦a hß║Īt nh├ón con Y tß║Īo th├Ānh:
+) Mß╗Śi hß║Īt nh├ón mß║╣ bß╗ŗ ph├ón r├Ż tß║Īo th├Ānh mß╗Öt hß║Īt nh├ón con n├¬n sß╗æ hß║Īt nh├ón con tß║Īo th├Ānh ─æ├║ng bß║▒ng sß╗æ hß║Īt nh├ón mß║╣ bß╗ŗ ph├ón r├Ż (hay sß╗æ mol hß║Īt nh├ón con tß║Īo th├Ānh bß║▒ng sß╗æ mol hß║Īt nh├ón mß║╣ ─æ├Ż ph├ón r├Ż):
\(\left\{ \begin{align}
& {{N}_{Y}}=\Delta {{N}_{X}}={{N}_{oX}}\left( 1-{{2}^{-\frac{t}{T}}} \right) \\
& {{n}_{Y}}=\Delta {{n}_{X}}={{n}_{oX}}\left( 1-{{2}^{-\frac{t}{T}}} \right) \\
\end{align} \right.\)
+) Khß╗æi lŲ░ß╗Żng hß║Īt nh├ón con Y ─æŲ░ß╗Żc tß║Īo th├Ānh sau thß╗Øi gian t l├Ā
\({{n}_{Y}}={{n}_{oX}}\left( 1-{{2}^{-\frac{t}{T}}} \right)\Rightarrow \frac{{{m}_{Y}}}{{{A}_{Y}}}=\frac{{{m}_{o}}}{{{A}_{X}}}\left( 1-{{2}^{-\frac{t}{T}}} \right)\Rightarrow {{m}_{Y}}={{m}_{o}}\left( 1-{{2}^{-\frac{t}{T}}} \right)\frac{{{A}_{Y}}}{{{A}_{X}}}\)
Trong ─æ├│: \({{n}_{Y}}\) l├Ā sß╗æ mol hß║Īt nh├ón con tß║Īo th├Ānh, \({{n}_{oX}}\) l├Ā sß╗æ mol ban ─æß║¦u cß╗¦a chß║źt ph├│ng xß║Ī.
\({{A}_{X}},{{A}_{Y}}\) l├Ā sß╗æ khß╗æi cß╗¦a chß║źt ph├│ng xß║Ī ban ─æß║¦u v├Ā chß║źt mß╗øi ─æŲ░ß╗Żc tß║Īo th├Ānh.
- Tß╗ē sß╗æ hß║Īt (khß╗æi lŲ░ß╗Żng) nh├ón con v├Ā sß╗æ hß║Īt (khß╗æi lŲ░ß╗Żng) nh├ón mß║╣ ß╗¤ thß╗Øi ─æiß╗ām t:
\(\left\{ \begin{align}
& {{N}_{X}}={{N}_{o}}{{.2}^{-\frac{t}{T}}} \\
& {{N}_{Y}}=\Delta {{N}_{X}}={{N}_{o}}\left( 1-{{2}^{-\frac{t}{T}}} \right) \\
\end{align} \right.\Rightarrow \frac{{{N}_{Y}}}{{{N}_{X}}}={{2}^{\frac{t}{T}}}-1\)
\(\Rightarrow \frac{{{m}_{Y}}}{{{m}_{X}}}=\frac{{{A}_{Y}}.{{N}_{Y}}}{{{A}_{X}}.{{N}_{X}}}=\frac{{{A}_{Y}}}{{{A}_{X}}}\left( {{2}^{\frac{t}{T}}}-1 \right).\)
V├Ł dß╗ź minh hß╗Źa: Chß║źt polonium \(_{84}^{210}Po\) ph├│ng xß║Ī anpha \(\left( \alpha \right)\) v├Ā chuyß╗ān th├Ānh ch├¼ \(_{82}^{206}Pb\)vß╗øi chu kß╗│ b├Īn r├Ż l├Ā 138,4 ng├Āy. Khß╗æi lŲ░ß╗Żng ban ─æß║¦u cß╗¦a Po l├Ā 50g.
a) Sau 100 ng├Āy (kß╗ā tß╗½ thß╗Øi ─æiß╗ām ban ─æß║¦u) th├¼ tß╗ē sß╗æ cß╗¦a sß╗æ hß║Īt nh├ón Pb v├Ā Po bß║▒ng bao nhi├¬u?
b) Sau bao l├óu khß╗æi lŲ░ß╗Żng hß║Īt nh├ón Po gß║źp 4 lß║¦n khß╗æi lŲ░ß╗Żng hß║Īt nh├ón Pb.
Lß╗Øi giß║Żi
PhŲ░ŲĪng tr├¼nh phß║Żn ß╗®ng: \(_{84}^{210}Po\to _{2}^{4}\alpha +_{82}^{206}Pb.\)
a) Ta c├│: \(\frac{{{N}_{Pb}}}{{{N}_{Po}}}={{2}^{\frac{t}{T}}}-1={{2}^{\frac{100}{138,4}}}-1\approx 0,6524\)
b) Ta c├│: \(\frac{{{m}_{Pb}}}{{{m}_{Po}}}=\frac{{{A}_{Pb}}}{{{A}_{Po}}}\left( {{2}^{\frac{t}{T}}}-1 \right)\Leftrightarrow \frac{1}{4}=\frac{206}{210}\left( {{2}^{\frac{t}{138,4}}}-1 \right)\Rightarrow t=45,1977\)ng├Āy.
2.3. Dß║ĀNG 3: Sß╗É Hß║ĀT NH├éN PH├éN R├ā ß╗× HAI THß╗£I ─ÉIß╗éM KH├üC NHAU.
B├Āi to├Īn: M├Īy ─æß║┐m xung cß╗¦a mß╗Öt chß║źt ph├│ng xß║Ī, trong lß║¦n ─æo thß╗® nhß║źt ─æß║┐m ─æŲ░ß╗Żc \(\Delta {{N}_{1}}\) hß║Īt nh├ón ph├ón r├Ż trong khoß║Żng thß╗Øi gian \(\Delta {{t}_{1}}\). Lß║¦n ─æo thß╗® hai sau lß║¦n ─æo thß╗® nhß║źt l├Ā t , m├Īy ─æß║┐m ─æŲ░ß╗Żc \(\Delta {{N}_{2}}\) ph├ón r├Ż trong c├╣ng khoß║Żng thß╗Øi gian \(\Delta {{t}_{2}}.\)
- Ph├ón bß╗æ sß╗æ hß║Īt nh├ón mß║╣ ph├│ng xß║Ī c├▓n lß║Īi theo trß╗źc thß╗Øi gian:
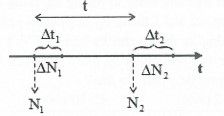
Gß╗Źi \({{N}_{1}}\) l├Ā sß╗æ hß║Īt nh├ón cß╗¦a chß║źt ph├│ng xß║Ī khi ─æo ß╗¤ lß║¦n thß╗® nhß║źt. Sß╗æ ph├ón r├Ż trong khoß║Żng thß╗Øi gian \(\Delta t\) ß╗¤ lß║¦n ─æo ─æß║¦u ti├¬n l├Ā: \(\vartriangle {{N}_{1}}={{N}_{1}}\left( 1-{{2}^{-\frac{\vartriangle {{t}_{1}}}{T}}} \right)={{N}_{1}}\left( 1-{{e}^{-\lambda .\vartriangle {{t}_{1}}}} \right).\)
Gß╗Źi \({{N}_{2}}\) l├Ā sß╗æ hß║Īt nh├ón ph├│ng xß║Ī khi ─æo ß╗¤ lß║¦n thß╗® hai. Sß╗æ ph├ón r├Ż trong khoß║Żng thß╗Øi gian \(\Delta t\) ß╗¤ lß║¦n ─æo thß╗® hai l├Ā: \(\Delta {{N}_{2}}={{N}_{2}}\left( 1-{{2}^{-\frac{\Delta {{t}_{2}}}{T}}} \right)={{N}_{2}}\left( 1-{{e}^{-\lambda .\Delta {{t}_{2}}}} \right).\)
Lß║Łp tß╗ē sß╗æ: \(\frac{\Delta {{N}_{1}}}{\Delta {{N}_{2}}}=\frac{{{N}_{1}}\left( 1-{{e}^{-\lambda .\vartriangle {{t}_{1}}}} \right)}{{{N}_{2}}\left( 1-{{e}^{-\lambda .\vartriangle {{t}_{2}}}} \right)}\)
Mß║Ęt kh├Īc, khi ─æo lß║¦n thß╗® 2 th├¼ sß╗æ hß║Īt ban ─æß║¦u cß╗¦a lß║¦n 2 ch├Łnh bß║▒ng sß╗æ hß║Īt c├▓n lß║Īi sau khi ─æo lß║¦n 1 mß╗Öt khoß║Żng thß╗Øi gian t, tß╗®c l├Ā: \({{N}_{2}}={{N}_{1}}{{.2}^{-\frac{t}{T}}}\)
Do đó: \(\frac{\Delta {{N}_{1}}}{\Delta {{N}_{2}}}={{2}^{\frac{t}{T}}}.\frac{1-{{e}^{-\lambda .\vartriangle {{t}_{1}}}}}{1-{{e}^{-\lambda .\vartriangle {{t}_{2}}}}}\left( 1 \right)\)
Tß╗½ to├Īn hß╗Źc: x rß║źt nhß╗Å: \(\frac{{{e}^{x}}-1}{x}\approx 1\Rightarrow {{e}^{x}}-1\approx x\Leftrightarrow {{e}^{-x}}-1\approx -x\Rightarrow 1-{{e}^{-x}}\approx x\Rightarrow \left\{ \begin{align} & 1-{{e}^{-\lambda .\vartriangle {{t}_{1}}}}\approx \lambda .\Delta {{t}_{1}} \\ & 1-{{e}^{-\lambda .\vartriangle {{t}_{2}}}}\approx \lambda .\Delta {{t}_{2}} \\ \end{align} \right.\)
\(\left( 1 \right)\Leftrightarrow \left( 2 \right)\)
Chß╗ē ├Īp dß╗źng c├┤ng thß╗®c (2) khi \(\Delta {{t}_{1}},\Delta {{t}_{2}}\ll t\).
V├Ł dß╗ź minh hß╗Źa: Ban ─æß║¦u, mß║½u ph├│ng xß║Ī C├┤ban c├│ \({{10}^{14}}\) hß║Īt ph├ón r├Ż trong ng├Āy ─æß║¦u ti├¬n (chu kß╗│ b├Īn r├Ż l├Ā T = 4 n─ām). Sau 12 n─ām, sß╗æ hß║Īt nh├ón C├┤ban ph├ón r├Ż trong 2 ng├Āy l├Ā
A. \(2,{{7.10}^{13}}\)hß║Īt.
B. \(3,{{3.10}^{13}}\)hß║Īt.
C. \({{5.10}^{13}}\)hß║Īt.
D. \(6,{{25.10}^{13}}\)hß║Īt.
Lß╗Øi giß║Żi
├üp dß╗źng:\(\frac{\Delta {{N}_{1}}}{\Delta {{N}_{2}}}={{2}^{\frac{t}{T}}}.\frac{\Delta {{t}_{1}}}{\Delta {{t}_{2}}}\Leftrightarrow \frac{{{10}^{14}}}{\Delta {{N}_{2}}}={{2}^{\frac{12}{4}}}.\frac{1}{2}\Rightarrow \Delta {{N}_{2}}=2,{{5.10}^{13}}\).
Chß╗Źn A.
3. LUYỆN TẬP
C├óu 1: Trong qu├Ī tr├¼nh ph├│ng xß║Ī cß╗¦a mß╗Öt chß║źt, sß╗æ hß║Īt nh├ón ph├│ng xß║Ī
A. giß║Żm ─æß╗üu theo thß╗Øi gian.
B. giß║Żm theo ─æŲ░ß╗Øng hypebol.
C. kh├┤ng giß║Żm.
D. giß║Żm theo quy luß║Łt h├Ām sß╗æ m┼®.
C├óu 2: C├┤ng thß╗®c n├Āo dŲ░ß╗øi ─æ├óy kh├┤ng phß║Żi l├Ā c├┤ng thß╗®c cß╗¦a ─æß╗ŗnh luß║Łt ph├│ng xß║Ī?
A.\(N\left( t \right)={{N}_{o}}{{.2}^{-\frac{t}{T}}}\)
B. \(N\left( t \right)={{N}_{o}}{{.2}^{-\lambda t}}\)
C.\(N\left( t \right)={{N}_{o}}.{{e}^{-\lambda t}}\)
D. \({{N}_{o=}}N\left( t \right).{{e}^{\lambda t}}.\)
C├óu 3: Hß║▒ng sß╗æ ph├│ng xß║Ī \(\lambda \) v├Ā chu k├¼ b├Īn r├Ż T li├¬n hß╗ć vß╗øi nhau bß╗¤i hß╗ć thß╗®c n├Āo sau ─æ├óy?
A. \(\lambda T=\ln 2\)
B. \(\lambda =T.\ln 2\)
C. \(\lambda =\frac{T}{0,693}\)
D. \(\lambda =-\frac{0,963}{T}\)
C├óu 4: Sß╗æ nguy├¬n tß╗Ł chß║źt ph├│ng xß║Ī bß╗ŗ ph├ón hß╗¦y sau khoß║Żng thß╗Øi gian t ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c n├Āo dŲ░ß╗øi ─æ├óy?
A. \(\Delta N={{N}_{o}}{{2}^{-\frac{t}{T}}}\)
B. \(\Delta N={{N}_{o}}.{{e}^{-\lambda t}}\)
C. \(\Delta N={{N}_{o}}\left( 1-{{e}^{-\lambda t}} \right)\)
D. \(\Delta N=\frac{{{N}_{o}}}{T}\)
C├óu 5: Mß╗Öt chß║źt ph├│ng xß║Ī c├│ sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ban ─æß║¦u l├Ā \({{N}_{o}}\) sau 1 chu k├¼ b├Īn r├Ż, sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ph├│ng xß║Ī c├▓n lß║Īi l├Ā
A. \({{{N}_{o}}}/{2}\;\)
B. \({{{N}_{o}}}/{4}\;\)
C. \({{{N}_{o}}}/{3}\;\)
D. \(\frac{{{N}_{o}}}{\sqrt{2}}\)
C├óu 6: Mß╗Öt lŲ░ß╗Żng chß║źt ph├│ng xß║Ī c├│ sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ban ─æß║¦u l├Ā \({{N}_{o}}\) sau 2 chu k├¼ b├Īn r├Ż, sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ph├│ng xß║Ī c├▓n lß║Īi l├Ā
A. \({{{N}_{o}}}/{2}\;\)
B. \({{{N}_{o}}}/{4}\;\)
C. \({{{N}_{o}}}/{8}\;\)
D. \(\frac{{{N}_{o}}}{\sqrt{2}}\)
C├óu 7: Mß╗Öt lŲ░ß╗Żng chß║źt ph├│ng xß║Ī c├│ sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ban ─æß║¦u l├Ā \({{N}_{o}}\) sau 3 chu k├¼ b├Īn r├Ż, sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ph├│ng xß║Ī c├▓n lß║Īi l├Ā
A. \({{{N}_{o}}}/{3}\;\)
B. \({{{N}_{o}}}/{9}\;\)
C. \({{{N}_{o}}}/{8}\;\)
D. \(\frac{{{N}_{o}}}{\sqrt{3}}\)
C├óu 8: Mß╗Öt lŲ░ß╗Żng chß║źt ph├│ng xß║Ī c├│ sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ban ─æß║¦u l├Ā \({{N}_{o}}\) sau 4 chu k├¼ b├Īn r├Ż, sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ph├│ng xß║Ī c├▓n lß║Īi l├Ā
A. \({{{N}_{o}}}/{4}\;\)
B. \({{{N}_{o}}}/{8}\;\)
C. \({{{N}_{o}}}/{16}\;\)
D. \({{{N}_{o}}}/{32}\;\)
C├óu 9: Mß╗Öt lŲ░ß╗Żng chß║źt ph├│ng xß║Ī c├│ sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ban ─æß║¦u l├Ā \({{N}_{o}}\) sau 5 chu k├¼ b├Īn r├Ż, sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ph├│ng xß║Ī c├▓n lß║Īi l├Ā
A. \({{{N}_{o}}}/{5}\;\)
B. \({{{N}_{o}}}/{25}\;\)
C. \({{{N}_{o}}}/{32}\;\)
D. \({{{N}_{o}}}/{50}\;\)
C├óu 10: Mß╗Öt lŲ░ß╗Żng chß║źt ph├│ng xß║Ī c├│ sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ban ─æß║¦u l├Ā \({{N}_{o}}\) sau 3 chu k├¼ b├Īn r├Ż, sß╗æ lŲ░ß╗Żng hß║Īt nh├ón ─æ├Ż bß╗ŗ ph├ón r├Ż l├Ā
A. \({{{N}_{o}}}/{3}\;\)
B. \({{{N}_{o}}}/{9}\;\)
C. \({{{N}_{o}}}/{8}\;\)
D. \(\frac{7{{N}_{o}}}{8}\)
---─Éß╗ā xem ─æß║¦y ─æß╗¦ nß╗Öi dung tß╗½ c├óu 11 ─æß║┐n c├óu 70, vui l├▓ng ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā xem online hoß║Ęc tß║Żi vß╗ü m├Īy t├Łnh---
Tr├¬n ─æ├óy l├Ā tr├Łch dß║½n mß╗Öt phß║¦n nß╗Öi dung t├Āi liß╗ću Ph├│ng xß║Ī v├Ā c├Īc dß║Īng b├Āi tß║Łp vß╗ü ph├│ng xß║Ī m├┤n Vß║Łt L├Į 12 n─ām 2021-2022. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm













