Một số bài toán thực tế liên quan đến hình học lớp 12 năm 2020

 MỘT SỐ BÀI TOÁN THỰC TẾ LIÊN QUAN ĐẾN HÌNH HỌC LỚP 12 NĂM 2020

A. Nội dung kiến thức.

Bài toán thực tế liên quan đến hình học thường xoay quanh một số nội dung như sau: Tính toán để đường đi được ngắn nhất, tính toán để diện tích được lớn nhất, hay cũng có thể đơn giản là tính diện tích hoặc thể tích của một vật…

Ta chú ý một số kiến thức sau:

 1. Công thức tính chu vi, diện tích của các hình, thể tích của các khối hình.

* Hình tam giác: Cho tam giác ABC đường cao AH, đặt a = BC, b = CA, c = AB, h = AH.

Chu vi tam giác là : P = a + b + c.

Diện tích tam giác là :

\(S = \frac{1}{2}ah = \frac{1}{2}ab.\sin C = \sqrt {p(p - a)(p - b)(p - c)} \)

( với \(p = \frac{P}{2}\)).

* Hình quạt: Xét hình quạt OAB có bán kính R, góc ở tâm bằng \(\alpha\) (tính theo radian).

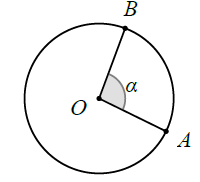
Chu vi của hình quạt là: \(P = 2\pi R.\frac{\alpha }{{2\pi }} \Leftrightarrow P = \alpha R.\)

Diện tích của hình quạt là: \(S = 2\pi {R^2}.\frac{\alpha }{{2\pi }} \Leftrightarrow S = \alpha {R^2}.\)

* Hình nón, khối nón:

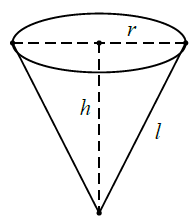
Diện tích xung quanh của hình nón có bán kính đường tròn đáy bằng r và có độ dài đường sinh bằng l là: \({S_{xq}} = \pi rl.\)

Diện tích toàn phần của hình nón tròn xoay bằng diện tích xung quanh của hình nón cộng với diện tích đáy của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}\)

Thể tích của khối nón tròn xoay có có chiều cao h và bán kính đáy bằng r là: \(V = \frac{1}{3}\pi {r^2}h.\)

*Hình trụ, khối trụ:

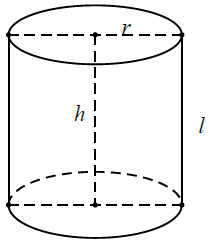
Diện tích xuang quanh của hình trụ có bán kính đáy bằng r và có đường sinh bằng l là: \({S_{xq}} = 2\pi rl.\)

Diện tích toàn phần của hình trụ bằng diện tích xung quanh của hình trụ đó cộng với diện tích hai đáy của hình trụ: \({S_{tp}} = 2\pi rl + 2\pi {r^2}.\)

Thể tích của khối trụ có chiều cao h và có bán kính đáy bằng r là: \(V = \pi {r^2}h.\)

Chú ý: Trường hợp hình lăng trụ đứng và khối lăng trụ đứng (như hình vẽ) thì h = l.

*Mặt cầu, khối cầu:

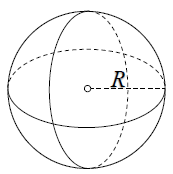
Mặt cầu bán kính R có diện tích là: \(S = 4\pi {R^2}.\)

Khối cầu bán kính R có thể tích là: \(S = \frac{4}{3}\pi {R^3}.\)

2. Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một đoạn, khoảng, nửa đoạn, nửa khoảng.

Có lẽ đây là một bài toán khá quen thuộc với rất nhiều bạn đọc, tác giả sẽ không nhắc lại phương pháp khảo sát hàm số để tìm giá trị lớn nhất và nhỏ nhất. Tác giả cung cấp thêm cho bạn đọc một số công thức sau:

• Cho hàm số \(y = a{x^2} + bx + c,\) nếu  a > 0 thì hàm số đã cho đạt giá trị nhỏ nhất trên R khi \(x = \frac{{ - b}}{{2a}}.\)
• Cho hàm số \(y = a{x^2} + bx + c,\) nếu a < 0 thì hàm số đã cho đạt giá trị lớn nhất trên R khi \(x = \frac{{ - b}}{{2a}}.\)
• Với a , b  là các số thực dương thì ta có: \(\sqrt {ab} \le \frac{{a + b}}{2} \Rightarrow ab \le \frac{{{{(a + b)}^2}}}{4}\) Đẳng thức xảy ra khi a = b.
• Với a , b, c  là các số thực dương thì ta có: \(\sqrt[3]{{abc}} \le \frac{{a + b + c}}{3} \Rightarrow abc \le \frac{{{{(a + b + c)}^3}}}{{27}}\)Đẳng thức xảy ra khi a = b = c.

Phần chứng minh xin để lại cho bạn đọc.

3. Ứng dụng của tích phân trong việc tính diện tích hình phẳng, tính thể tích của khối tròn xoay.

• Nếu hàm số y = f(x)  liên tục trên đoạn [ a;b] thì diện tích S của hình phẳng giới hạn bởi các đường : \(y = f(x),y = 0,x = a,x = b\) là \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
• Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số \(y = f(x) = g(x)\) liên tục trên đoạn [ a; b] và hai đường thẳng x = a, x = b là \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)
• Cho hàm số y = f(x) liên tục trên [a , b]. Thể tích V của khối tròn xoay tạo bởi hình phẳng giới hạn bởi các đường \(y = f(x),y = 0,x = a,x = b,\): khi quay xung quanh trục hoành được tính theo công thức : \(V = \pi \int\limits_a^b {{f^2}(x)dx.} \) 
•  Thể tích V của khối tròn xoay tạo bởi hình phẳng giới hạn bởi các đường \(y = f(x),y = g(x),(0 \le f(x) \le g(x);f;g\) liên tục trên đoạn [a;b]), x = a, x = b , khi quay xung quanh trục Ox được tính theo công thức : \(V = \pi \int\limits_a^b {\left| {{g^2}(x) - {f^2}(x)} \right|dx.} \)

B. Ví dụ minh hoạ.

Lời giải

Giả sử  \(AS = x,0 < x < 4 \Rightarrow BS = 4 - x.\)

Tổng chi phí mắc đường dây điện là : \(f(x) = 300x + 500\sqrt {1 + {{(4 - x)}^2}} \).

Bài toán trở thành tìm giá trị lớn nhất của f(x) trên (0;4).

Cách 1: Ta có:

\(F'(x) = 0 \Leftrightarrow 300 + 500\frac{{ - (4 - x)}}{{\sqrt {1 + {{(4 - x)}^2}} }} = 0 \\\Leftrightarrow 3\sqrt {1 + {{(4 - x)}^2}} = 5(4 - x) \\ \Leftrightarrow {(x - 4)^2} = \frac{9}{{16}} \\\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \frac{{13}}{4}}\\ {x = \frac{{19}}{4}} \end{array}} \right.\)

So sánh với điều kiện ta có \(x = \frac{{13}}{4} = 3,25.\)

Đáp án A.

Cách 2:

Ta có: Ta có: f (3,25) =1600; f (1) =1881,13883; f (2) =1718,033989; f (1,5) =1796,291202.

Như vậy ta cũng tìm ra A là đáp án.

Bình luận: Không ít bạn đọc cho rằng cách giải thứ hai không được khoa học và làm mất đi vẻ đẹp của toán học. Quan điểm của tác giả về Cách 1 và Cách 2 như sau:

• Cả hai cách đều phải tìm giá trị lớn nhất của f (x) trên (0;4).
• Cách 1: Chúng ta giải quyết bằng cách khảo sát hàm số f (x) trên khoảng (0;4) để tìm ra giá trị của x mà tại đó f (x) đạt giá trị lớn nhất; tiếp theo, so sánh kết quả tìm được với các đáp án A, B, C, D để tìm ra câu trả lời đúng cho câu hỏi.
• Cách 2: Sau khi lập được hàm số f (x) như Cách 1, tính f (3,25), f (1), f (2), f (1,5); số lớn nhất trong bốn số tính được sẽ là giá trị lớn nhất của f (x). Từ đó, hiển nhiên, dễ dàng tìm ra câu trả lời đúng cho câu hỏi.

Có thể thấy, rõ ràng Cách 2 giúp ta tìm đáp án nhanh hơn cách 1. Sự khác biệt giữa Cách 1 và Cách 2 nêu trên nằm ở quan niệm về tình huống đặt ra. Với Cách 1, ta coi các phương án A, B, C, D chỉ là các dữ liệu đưa ra để đối chiếu; với Cách 2, ta coi các phương án A, B, C, D là giả thiết của tình huống đặt ra.

• Có lẽ những bài tập trắc nghiệm có thể làm theo Cách 2 đôi phần là hạn chế của việc kiểm tra theo hình thức trắc nghiệm, tuy nhiên trong quá trình làm bài thi mỗi câu hỏi đã được người ra đề đã ngầm ấn định khoảng thời gian làm bài, do vậy theo tác giả nếu gặp câu hỏi này trong phòng thi học sinh nên làm theo Cách 2.

Lời giải

Gọi độ dài IA và AB lần lượt là a và b ( 0 < a, b < 4).

Vì chu vi của cửa sổ bằng 4m nên ta có:

\(\pi a + (2a + 2b) = 4 \Leftrightarrow b = \frac{{4 - \pi a - 2a}}{2}(1).\)

Diện tích của cửa sổ là:

\(S(a) = \frac{{\pi {a^2}}}{2} + 2a.\frac{{4 - \pi a - 2a}}{2} \\\Leftrightarrow S(a) = 4a - 2{a^2} - \frac{{\pi {a^2}}}{2} = - \left( {2 + \frac{\pi }{2}} \right){a^2} + 4a.\)

Bài toán trở thành tìm giá trị lớn nhất của S(a) trên (0;4).

Cách 1:

Ta có: \(S'(a) = 0 \Leftrightarrow 4 - 4a - \pi a = 0 \Leftrightarrow a = \frac{4}{{4 + \pi }}.\) 

Suy ra: \(\mathop {{\rm{max}}}\limits_{0 < x < 4} S(a) = S\left( {\frac{4}{{4 + \pi }}} \right) = \frac{8}{{4 + \pi }}.\)

Đáp án B.

Cách 2:

Do S(a) là hàm số bậc hai có hệ số của a² âm nên nó đạt giá trị lớn nhất khi:

\(a = - \frac{4}{{2.\left[ { - \left( {2 + \frac{\pi }{2}} \right)} \right]}} \\\Leftrightarrow a = \frac{4}{{4 + \pi }} \\\Rightarrow \mathop {{\rm{max}}}\limits_{0 < x < 4} S(a) = S\left( {\frac{4}{{4 + \pi }}} \right) = \frac{8}{{4 + \pi }}.\)

Đáp án B.

Bình luận: Vì sao tại (1) chúng ta không biểu diễn a theo b mà lại biểu diễn b theo a? Đâu đó có bạn đọc nghĩ rằng việc biểu diễn a theo b hay biểu diễn b theo a thì các bước làm vẫn vậy và không ảnh hưởng đến quá trình làm bài. Liệu điều này có đúng? Câu trả lời là không? Chúng ta biết rằng cửa gồm hai bộ phận (bộ phận hình chữ nhật và bộ phận có dạng nửa đường tròn), nhưng cả hai bộ phận này khi tính diện tích đều phải tính theo a. Như vậy nếu chúng ta biểu diễn a theo b thì việc tính toán sẽ phức tạp hơn khi biểu diễn b theo a. Công việc tưởng chừng như rất đơn giản này nhưng nó có thể giúp ích rất nhiều cho bạn đọc trong khi tính toán.

...

Trên đây là trích dẫn một phần nội dung tài liệu Một số bài toán thực tế liên quan đến hình học lớp 12 năm 2020. Để xem toàn bộ nội dung, các em vui lòng đăng nhập vào trang hoc247.net để tham khảo và tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Chúc các em học tập tốt !