Đề cương ôn tập giữa HK2 môn Toán 12 năm 2022-2023

SỞ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG THPT QUANG TRUNG

ĐỀ CƯƠNG ÔN TẬP THI GIỮA HỌC KÌ 2 NĂM HỌC 2022-2023 MÔN TOÁN LỚP 12

Câu 1:  Tích phân \(Oxyz\) bằng

A.  \(A\left( 2\,;\,-1\,;\,2 \right)\).                                  

B.  \(B\left( 0\,;\,1\,;\,0 \right)\).                                    

C.  \(AB\).

D.  \({{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-1 \right)}^{2}}=12\).

Câu 2:  Nếu \({{\left( x+2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+2 \right)}^{2}}=2\) và \({{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-1 \right)}^{2}}=\sqrt{3}\) có đạo hàm liên tục thì

A.  \({{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-1 \right)}^{2}}=3\)       

B.  \({F\left( x \right)}\)

C.  \({f\left( x \right)=\sin x+\cos x}\)                           

D.  \({F\left( 0 \right)=1}\)

Câu 3:  Trong không gian \({F\left( x \right)}\), mặt cầu \(-\cos x+\sin x+2\) có tâm \(-\cos x+\sin x-2\) và bán kính bằng \(-\cos x+\sin x+1\). Phương trình của \(\cos x-\sin x+1\) là

A.  \(f\left( x \right)=x+\sin 3x\).                                  

B.  \(\frac{{{x}^{2}}}{2}-\text{3cos}3x+C\).

C.  \(\frac{{{x}^{2}}}{2}-\frac{1}{3}\text{cos}3x+C\).

D.  \(\frac{{{x}^{2}}}{2}+\frac{1}{3}\text{cos}3x+C\).

Câu 4:  Cho \(\frac{{{x}^{2}}}{2}+3\text{cos}3x+C\) và \(I=\int\limits_{-1}^{2}{f\left( x \right)}\text{dx=3}\). Khi đó \(J=\int\limits_{-1}^{2}{\left[ 3f\left( x \right)-4 \right]\text{dx}}\) bằng

A.  17.                                

B.  1.                                  

C.  \(-3\).                            

D.  \(-1\).

Câu 5:  Hàm số \(5\) là một nguyên hàm của hàm số \(2\) trên khoảng \(\int\limits_{5}^{2}{f\left( x \right)}\text{d}x=2\) nếu

A.  \(\int\limits_{2}^{5}{3f\left( x \right)}\text{d}x\).  

B.  \(3\).

C.  \(6\).                                                                         

D.  \(12\).

Câu 6:  Trong không gian \(-6\), mặt cầu \(f\left( x \right)=\frac{\ln x}{x}\) có bán kính bằng

A.  \(\ln \left( \ln x \right)+C\).

B.  \(\frac{1}{2}{{\ln }^{2}}x+C\).                               

C.  \(\frac{1}{2}{{\ln }^{2}}x+\ln x+C\).                  

D.  \({{\ln }^{2}}x+C\).

Câu 7:  Khẳng định nào sau đây đúng?

A.  \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x=8}\).      

B.  \(\int\limits_{1}^{5}{f\left( x \right)\text{d}x=-3}\).

C.  \(\int\limits_{0}^{5}{f\left( x \right)\text{d}x}\). 

D.  \(-11\).

Câu 8:  Cho hàm số \(-\frac{8}{3}\) có đạo hàm trên \(Oxyz\), \(\overrightarrow{OM}=2\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}\) và \(M\). Tính \(\left( Oxy \right)\)

A.  \({{M}_{3}}\left( 2;-3;0 \right)\)                             

B.  \({{M}_{1}}\left( 2;0;0 \right)\)                               

C.  \({{M}_{4}}\left( 2;0;1 \right)\)                              

D.  \({{M}_{2}}\left( 0;0;1 \right)\)

Câu 9:  Họ nguyên hàm của hàm số \(\int\limits_{0}^{m}{\left( 3{{x}^{2}}-2x+1 \right)}\text{d}x=6\) là:

A.  \(\left( -\infty ;0 \right)\).                                        

B.  \(\left( -3;1 \right)\).     

C.  \(\left( 0;4 \right)\).

D.  \(\left( -1;2 \right)\).

Câu 10:  Tích phân \(\int\limits_{0}^{1}{{{x}^{2023}}dx}\) bằng

A.  \(\int{\frac{{f}'\left( \sqrt{x} \right)}{\sqrt{x}}}\text{d}x\).                              

B.  \(f\left( \sqrt{x} \right)+C\).                                   

C.\(\frac{1}{2023}\).        

D.  \(\frac{1}{2024}\).

Câu 11:  Cho hai hàm số \(\frac{1}{2}f\left( \sqrt{x} \right)+C\) và \(f(x)=\frac{{{x}^{2}}}{\sqrt{{{x}^{3}}+1}}\) liên tục trên \(\frac{1}{3}\sqrt{{{x}^{3}}+1}+C.\), \(\frac{2}{3}\sqrt{{{x}^{3}}+1}+C.\). Khẳng định nào sau đây là khẳng định sai?

A.  \(\frac{2}{3\sqrt{{{x}^{3}}+1}}+C.\).                    

B.  \(\frac{1}{3\sqrt{{{x}^{3}}+1}}+C.\).

C.  \(Oxyz\).                                                                  

D.  \(A\left( 2\,;\,1\,;\,3 \right)\).

Câu 12:  Giả sử \(B\left( 1\,;\,-2\,;\,2 \right)\) là hàm số liên tục trên khoảng \(C\left( x\,;\,y\,;\,5 \right)\) và \(x+y\) là ba số bất kỳ trên khoảng \(3\). Khẳng định nào sau đây sai?

A.  \(10\).                                                                       

B.  \(12\).

C.  \(11\).                                                                       

D.  \(Oxyz\).

Câu 13:  Cho 2 hàm số \(A\left( -2\,;\,3\,;\,-1 \right)\) và \(B\left( -4\,;\,1\,;\,9 \right)\) có đạo hàm liên tục trên khoảng \(I\). Khẳng định nào sau đây đúng?

A.  \(AB\).                                                                     

B.  \(\left( -3\,;\,2\,;\,4 \right)\).

C.  \(\left( -2\,;\,-2\,;\,10 \right)\).                                  

D.  \(\left( -3\,;\,2\,;\,-4 \right)\).

Câu 14:  Nguyên hàm của hàm số \(f(x)=3x^2+1\) là

A.  \(6x+C\).                        

B.  \({x^3\over 3} +x+C\).                   

C.  \({x^3} +x+C\).                   

D.  \({x^3}+C\).

Câu 15:  Trong không gian \(\left( -6\,;\,4\,;\,8 \right)\), cho mặt cầu \(I=\int\limits_{1}^{2}{\frac{1}{2x-1}\text{d}x}\). Tâm của \(I=\frac{\ln 3-1}{2}\)là điểm nào sau đây?

A.  \(I=\ln 3+1\)                 

B.  \(I=\frac{\ln 3}{3}\)      

C.  \(I=\frac{\ln 3}{2}\)     

D.  \(\left( 1;1;1 \right)\)

Câu 16:  Mệnh đề nào sau đây là đúng ?

A.  \(\int{x{{e}^{x}}}\text{d}x={{e}^{x}}+x{{e}^{x}}+C\).  

B.  \(\int{x{{e}^{x}}}\text{d}x=\frac{{{x}^{2}}}{2}{{e}^{x}}+{{e}^{x}}+C\).

C.  \(\int{x{{e}^{x}}}\text{d}x=\frac{{{x}^{2}}}{2}{{e}^{x}}+C\).  

D.  \(\int{x{{e}^{x}}\text{d}x}=x{{e}^{x}}-{{e}^{x}}+C\).

Câu 17:  Biết \(\int{f\left( x \right)dx}=F\left( x \right)+C\).Trong các khẳng định sau, khẳng định nào đúng?

A. \(\int\limits_{a}^{b}{f\left( x \right)dx}=F\left( b \right)-F\left( a \right)\) .     

B.  \(\int\limits_{a}^{b}{f\left( x \right)dx}=F\left( b \right)+F\left( a \right)\).

C.  \(\int\limits_{a}^{b}{f\left( x \right)dx}=F\left( b \right).F\left( a \right)\).      

D.  \(\int\limits_{a}^{b}{f\left( x \right)dx}=F\left( a \right)-F\left( b \right)\).

Câu 18:  Trên khoảng \(\left( 0;+\infty  \right)\), hàm số \(F\left( x \right)=\ln x\) là một nguyên hàm của hàm số?

A.  \(f\left( x \right)=x\ln x-x\).                                    

B.  \(f\left( x \right)=x\ln x-x+C,C\in \mathbb{R}\).

C.  \(f\left( x \right)=\frac{1}{x}+C,C\in \mathbb{R}\).     

D.  \(f\left( x \right)=\frac{1}{x}\).

Câu 19:  Tìm họ nguyên hàm của hàm số \(f\left( x \right)={{\text{e}}^{3x}}\).

A.  \(\int{f\left( x \right)}\text{d}x={{\text{e}}^{3x}}+C\).                                     

B.  \(\int{f\left( x \right)}\text{d}x=\frac{1}{3}.{{\text{e}}^{3x}}\).                        

C.  \(\int{f\left( x \right)}\text{d}x=\ln \left| 3x \right|+C\).                                    

D.  \(\int{f\left( x \right)}\text{d}x=\frac{1}{3}.{{\text{e}}^{3x}}+C\).

Câu 20:  Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow{u}=-3\overrightarrow{i}+7\overrightarrow{j}+\overrightarrow{k}\). Tọa độ của vectơ \(\overrightarrow{u}\) là

A.  \(\left( 3;\,7\,;1 \right)\).

B.  \(\left( -3;\,7\,;1 \right)\).                                          

C.  \(\left( -3;\,7\,;0 \right)\).                                          

D.  \(\left( 3;\,7\,;0 \right)\).

---(Để xem tiếp nội dung của đề cương các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--

1	B	6	D	11	A	16	D	21	D	26	B	31	C	36	A
2	C	7	A	12	A	17	A	22	A	27	B	32	B	37	C
3	A	8	C	13	A	18	D	23	B	28	A	33	D	38	D
4	D	9	D	14	C	19	D	24	A	29	A	34	A	39	B
5	B	10	D	15	A	20	B	25	D	30	C	35	D	40	D

 

HƯỚNG DẪN GIẢI

Câu 37:

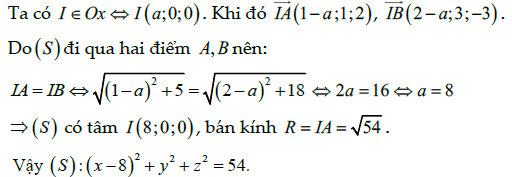
---(Để xem tiếp nội dung của đề cương các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--

 

Trên đây là một phần nội dung tài liệu Đề cương ôn tập giữa HK2 lớp 12 môn Toán năm 2022-2023. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hi vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.

Chúc các em học tốt!