HOC247 mß╗Øi qu├Į thß║¦y c├┤ v├Ā c├Īc em hß╗Źc sinh tham khß║Żo ─Éß╗ü cŲ░ŲĪng ├┤n tß║Łp giß╗»a HK1 m├┤n Toa╠ün 12 n─ām 2023-2024 ─æ├Ż ─æŲ░ß╗Żc HOC247 bi├¬n soß║Īn dŲ░ß╗øi ─æ├óy. Th├┤ng qua t├Āi liß╗ću n├Āy, c├Īc em c├│ thß╗ā kh├Īi qu├Īt hß╗ć thß╗æng kiß║┐n thß╗®c v├Ā r├©n luyß╗ćn k─® n─āng giß║Żi b├Āi tß║Łp ─æß╗ā l├Ām b├Āi thi thß║Łt tß╗æt. Ch├║c c├Īc em hß╗Źc sinh ─æß║Īt kß║┐t quß║Ż cao trong k├¼ thi giŲ░╠āa HK1 sß║»p tß╗øi!
1. T├┤╠ēng hŲĪ╠Żp ki├¬╠ün thŲ░╠üc
1.1. Gia╠ēi ti╠üch
1.1.1. Sß╗▒ ─æß╗ōng biß║┐n, nghß╗ŗch biß║┐n cß╗¦a h├Ām sß╗æ
Cho h├Ām sß╗æ \(y = f\left( x \right)\), khi ─æ├│:
+) \(f'\left( x \right) > 0\) tr├¬n khoß║Żng n├Āo th├¼ h├Ām sß╗æ ─æß╗ōng biß║┐n tr├¬n khoß║Żng ─æ├│.
+) \(f'\left( x \right) < 0\) tr├¬n khoß║Żng n├Āo th├¼ h├Ām sß╗æ nghß╗ŗch biß║┐n tr├¬n khoß║Żng ─æ├│.
─Éiß╗üu kiß╗ćn ─æß╗ā h├Ām sß╗æ ─æß╗ōng biß║┐n, nghß╗ŗch biß║┐n tr├¬n khoß║Żng \(\left( {a;b} \right)\)
+) ─Éß╗ā h├Ām sß╗æ ─æß╗ōng biß║┐n tr├¬n khoß║Żng \(\left( {a,b} \right)\) th├¼ \(f'\left( x \right) \ge 0,\forall x \in \left( {a,b} \right)\).
+) ─Éß╗ā h├Ām sß╗æ nghß╗ŗch biß║┐n tr├¬n khoß║Żng \(\left( {a,b} \right)\) th├¼ \(f'\left( x \right) \le 0,\forall x \in \left( {a,b} \right).\)
1.1.2. Cß╗▒c trß╗ŗ cß╗¦a h├Ām sß╗æ
Dß║źu hiß╗ću 1:
+) Nß║┐u \(f'\left( {{x_0}} \right) = 0\) hoß║Ęc \(f'\left( x \right)\) kh├┤ng x├Īc ─æß╗ŗnh tß║Īi \({x_0}\) v├Ā n├│ ─æß╗Ģi dß║źu tß╗½ dŲ░ŲĪng sang ├óm khi qua \({x_0}\) th├¼ \({x_0}\) l├Ā ─æiß╗ām cß╗▒c ─æß║Īi cß╗¦a h├Ām sß╗æ.
+) Nß║┐u \(f'\left( {{x_0}} \right) = 0\) hoß║Ęc \(f'\left( x \right)\) kh├┤ng x├Īc ─æß╗ŗnh tß║Īi \({x_0}\) v├Ā n├│ ─æß╗Ģi dß║źu tß╗½ ├óm sang dŲ░ŲĪng khi qua \({x_0}\) th├¼ \({x_0}\) l├Ā ─æiß╗ām cß╗▒c tiß╗āu cß╗¦a h├Ām sß╗æ.
- Quy tß║»c 1: (dß╗▒a v├Āo dß║źu hiß╗ću 1)
+) T├Łnh y'
+) T├¼m c├Īc ─æiß╗ām tß╗øi hß║Īn cß╗¦a h├Ām sß╗æ. (tß║Īi ─æ├│ \(y' = 0\) hoß║Ęc \(y'\) kh├┤ng x├Īc ─æß╗ŗnh)
+) Lß║Łp bß║Żng x├®t dß║źu \(y'\) v├Ā dß╗▒a v├Āo bß║Żng x├®t dß║źu v├Ā kß║┐t luß║Łn.
Dß║źu hiß╗ću 2:
Cho h├Ām sß╗æ \(y = f\left( x \right)\) c├│ ─æß║Īo h├Ām ─æß║┐n cß║źp 2 tß║Īi \({x_0}\).
+) \({x_0}\) l├Ā ─æiß╗ām cß╗▒c ─æß║Īi \( \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.\)
+) \({x_0}\) l├Ā ─æiß╗ām cß╗▒c tiß╗āu \(\Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right.\)
- Quy tß║»c 2: (dß╗▒a v├Āo dß║źu hiß╗ću 2)
+) T├Łnh \(f'\left( x \right),f''\left( x \right)\).
+) Giß║Żi phŲ░ŲĪng tr├¼nh \(f'\left( x \right) = 0\) t├¼m nghiß╗ćm.
+) Thay nghiß╗ćm vß╗½a t├¼m v├Āo \(f''\left( x \right)\) v├Ā kiß╗ām tra, tß╗½ ─æ├│ suy kß║┐t luß║Łn.
1.1.3. Gi├Ī trß╗ŗ lß╗øn nhß║źt v├Ā gi├Ī tß╗ŗ nhß╗Å nhß║źt cß╗¦a h├Ām sß╗æ
Quy tß║»c t├¼m GTLN ŌĆō GTNN cß╗¦a h├Ām sß╗æ:
- Quy tß║»c chung: (ThŲ░ß╗Øng d├╣ng cho D l├Ā mß╗Öt khoß║Żng)
+ T├Łnh \(f'\left( x \right)\), giß║Żi phŲ░ŲĪng tr├¼nh \(f'\left( x \right) = 0\) t├¼m nghiß╗ćm tr├¬n D.
+ Lß║Łp BBT cho h├Ām sß╗æ tr├¬n D.
+ Dß╗▒a v├Āo BBT v├Ā ─æß╗ŗnh ngh─®a tß╗½ ─æ├│ suy ra GTLN, GTNN.
- Quy tß║»c ri├¬ng: (D├╣ng cho \(\left[ {a;b} \right]\)) . Cho h├Ām sß╗æ \(y = f\left( x \right)\) x├Īc ─æß╗ŗnh v├Ā li├¬n tß╗źc tr├¬n \(\left[ {a;b} \right]\)
+ T├Łnh \(f'\left( x \right)\), giß║Żi phŲ░ŲĪng tr├¼nh \(f'\left( x \right) = 0\) t├¼m nghiß╗ćm tr├¬n \(\left[ {a,b} \right]\).
+ Giß║Ż sß╗Ł phŲ░ŲĪng tr├¼nh c├│ c├Īc nghiß╗ćm \({x_1},{x_2},... \in \left[ {a,b} \right]\).
+ T├Łnh c├Īc gi├Ī trß╗ŗ \(f\left( a \right),f\left( b \right),f\left( {{x_1}} \right),f\left( {{x_2}} \right),...\).
+ So s├Īnh ch├║ng v├Ā kß║┐t luß║Łn.
1.1.4. Tiß╗ćm cß║Łn cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ
+) ─ÉŲ░ß╗Øng thß║│ng \(x = a\) l├Ā TC─É cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y = f\left( x \right)\) nß║┐u c├│ mß╗Öt trong c├Īc ─æiß╗üu kiß╗ćn sau:
\(\mathop {\lim }\limits_{x \to {a^ + }} y = + \infty\) hoß║Ęc \(\mathop {\lim }\limits_{x \to {a^ + }} y = - \infty\) hoß║Ęc \(\mathop {\lim }\limits_{x \to {a^ - }} y = + \infty\) hoß║Ęc \(\mathop {\lim }\limits_{x \to {a^ - }} y = - \infty\)
+) ─ÉŲ░ß╗Øng thß║│ng y = b l├Ā TCN cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y = f\left( x \right)\) nß║┐u c├│ mß╗Öt trong c├Īc ─æiß╗üu kiß╗ćn sau:
\(\mathop {\lim }\limits_{x \to + \infty } y = b\) hoß║Ęc \(\mathop {\lim }\limits_{x \to - \infty } y = b\)
1.1.5. Bß║Żng biß║┐n thi├¬n v├Ā ─æß╗ō thß╗ŗ h├Ām sß╗æ
a) C├Īc dß║Īng ─æß╗ō thß╗ŗ h├Ām sß╗æ bß║Łc ba \(y = a{x^3} + b{x^2} + cx + d\)
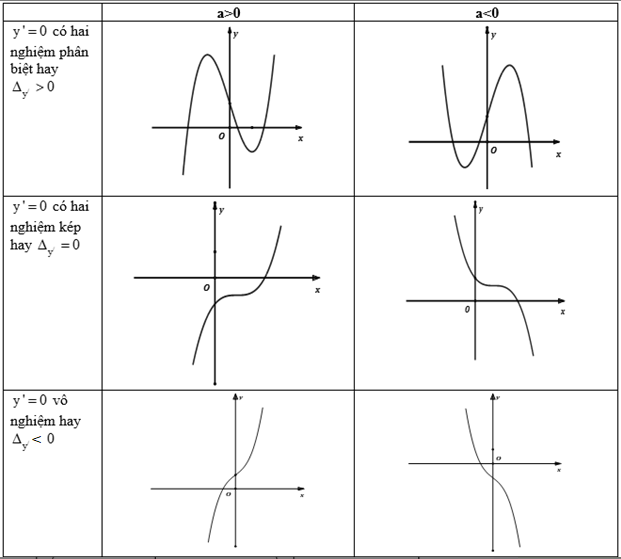
b) C├Īc dß║Īng ─æß╗ō thß╗ŗ h├Ām sß╗æ bß║Łc bß╗æn tr├╣ng phŲ░ŲĪng \(y = a{x^4} + b{x^2} + c\)
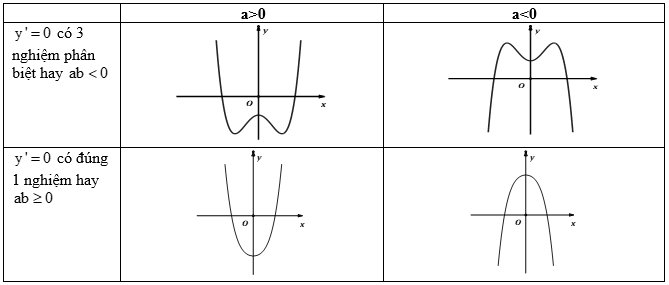
c) C├Īc dß║Īng ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y = \dfrac{{ax + b}}{{cx + d}}\)
+) Tß║Łp x├Īc ─æß╗ŗnh: \(D = R\backslash \left\{ { - \dfrac{d}{c}} \right\}\)
+) ─Éß║Īo h├Ām: \(y = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
- Nß║┐u \(ad - bc > 0\) h├Ām sß╗æ ─æß╗ōng biß║┐n tr├¬n tß╗½ng khoß║Żng x├Īc ─æß╗ŗnh. ─Éß╗ō thß╗ŗ nß║▒m g├│c phß║¦n tŲ░ 2 v├Ā 4.
- Nß║┐u \(ad - bc < 0\) h├Ām sß╗æ nghß╗ŗch biß║┐n tr├¬n tß╗½ng khoß║Żng x├Īc ─æß╗ŗnh. ─Éß╗ō thß╗ŗ nß║▒m g├│c phß║¦n tŲ░ 1 v├Ā 3.
+) ─Éß╗ō thß╗ŗ h├Ām sß╗æ c├│: TC─É: \(x = - \dfrac{d}{c}\) v├Ā TCN: \(y = \dfrac{a}{c}\)
+) ─Éß╗ō thß╗ŗ c├│ t├óm ─æß╗æi xß╗®ng: \(I\left( { - \dfrac{d}{c};\dfrac{a}{c}} \right)\)
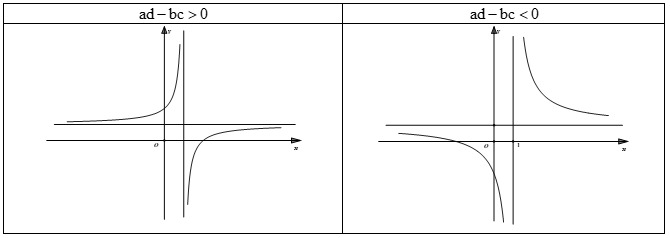
1.1.6. Sß╗▒ tŲ░ŲĪng giao cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ
a) T├¼m giao ─æiß╗ām cß╗¦a hai ─æß╗ō thß╗ŗ h├Ām sß╗æ
PhŲ░ŲĪng ph├Īp:
Cho 2 h├Ām sß╗æ \(y = f\left( x \right),y = g\left( x \right)\) c├│ ─æß╗ō thß╗ŗ lß║¦n lŲ░ß╗Żt l├Ā \(\left( C \right)\) v├Ā \(\left( {C'} \right).\)
+) Lß║Łp phŲ░ŲĪng tr├¼nh ho├Ānh ─æß╗Ö giao ─æiß╗ām cß╗¦a \(\left( C \right)\) v├Ā \(\left( {C'} \right):~f\left( x \right) = g\left( x \right)\,\,\,\left( * \right)\)
+) Giß║Żi phŲ░ŲĪng tr├¼nh t├¼m x tß╗½ ─æ├│ suy ra y v├Ā tß╗Źa ─æß╗Ö giao ─æiß╗ām.
+) Sß╗æ nghiß╗ćm cß╗¦a \(\left( * \right)\) l├Ā sß╗æ giao ─æiß╗ām cß╗¦a \(\left( C \right)\) v├Ā \(\left( {C'} \right).\)
b) TŲ░ŲĪng giao cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ bß║Łc ba
PhŲ░ŲĪng ph├Īp 1: Bß║Żng biß║┐n thi├¬n (PP ─æß╗ō thß╗ŗ)
+) Lß║Łp phŲ░ŲĪng tr├¼nh ho├Ānh ─æß╗Ö giao ─æiß╗ām dß║Īng \(F\left( {x,m} \right) = 0\) (phŲ░ŲĪng tr├¼nh ß║®n x tham sß╗æ m)
+) C├┤ lß║Łp m ─æŲ░a phŲ░ŲĪng tr├¼nh vß╗ü dß║Īng \(m = f\left( x \right)\)
+) Lß║Łp BBT cho h├Ām sß╗æ \(y = f\left( x \right)\).
+) Dß╗▒a v├Āo giß║Ż thiß║┐t v├Ā BBT tß╗½ ─æ├│ suy ra m.
Dß║źu hiß╗ću: Sß╗Ł dß╗źng PP bß║Żng biß║┐n thi├¬n khi m ─æß╗Öc lß║Łp vß╗øi x.
PhŲ░ŲĪng ph├Īp 2: Nhß║®m nghiß╗ćm ŌĆō tam thß╗®c bß║Łc 2.
+) Lß║Łp phŲ░ŲĪng tr├¼nh ho├Ānh ─æß╗Ö giao ─æiß╗ām \(F\left( {x,m} \right) = 0\)
+) Nhß║®m nghiß╗ćm: (Khß╗Ł tham sß╗æ). Giß║Ż sß╗Ł \(x = {x_0}\) l├Ā 1 nghiß╗ćm cß╗¦a phŲ░ŲĪng tr├¼nh.
+) Ph├ón t├Łch: \(F\left( {x,m} \right) = 0 \Leftrightarrow \left( {x - {x_0}} \right).g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_0}\\g\left( x \right) = 0\end{array} \right.\) (\(g\left( x \right) = 0\) l├Ā phŲ░ŲĪng tr├¼nh bß║Łc 2 ß║®n x tham sß╗æ m).
+) Dß╗▒a v├Āo y├¬u cß║¦u b├Āi to├Īn ─æi xß╗Ł l├Į phŲ░ŲĪng tr├¼nh bß║Łc 2 \(g\left( x \right) = 0\).
1.2. Hi╠Ćnh ho╠Żc
1.2.1. M├┤╠Żt s├┤╠ü ─æi╠Żnh nghi╠āa
H├¼nh l─āng trß╗ź ─æß╗®ng
- ─Éß╗ŗnh ngh─®a: H├¼nh l─āng trß╗ź ─æß╗®ng l├Ā h├¼nh l─āng trß╗ź c├│ cß║Īnh b├¬n vu├┤ng g├│c vß╗øi mß║Ęt ─æ├Īy.
- T├Łnh chß║źt: C├Īc mß║Ęt b├¬n cß╗¦a h├¼nh l─āng trß╗ź ─æß╗®ng l├Ā c├Īc h├¼nh chß╗» nhß║Łt v├Ā vu├┤ng g├│c vß╗øi mß║Ęt ─æ├Īy.
H├¼nh l─āng trß╗ź ─æß╗üu
- ─Éß╗ŗnh ngh─®a: H├¼nh l─āng trß╗ź ─æß╗üu l├Ā h├¼nh l─āng trß╗ź ─æß╗®ng c├│ ─æ├Īy l├Ā ─æa gi├Īc ─æß╗üu.
- T├Łnh chß║źt: C├Īc mß║Ęt b├¬n cß╗¦a h├¼nh l─āng trß╗ź ─æß╗üu l├Ā c├Īc h├¼nh chß╗» nhß║Łt bß║▒ng nhau v├Ā vu├┤ng g├│c vß╗øi mß║Ęt ─æ├Īy.
H├¼nh hß╗Öp ─æß╗®ng
- ─Éß╗ŗnh ngh─®a: H├¼nh hß╗Öp ─æß╗®ng l├Ā h├¼nh hß╗Öp c├│ cß║Īnh b├¬n vu├┤ng g├│c vß╗øi mß║Ęt ─æ├Īy.
- T├Łnh chß║źt: H├¼nh hß╗Öp ─æß╗®ng c├│ 2 ─æ├Īy l├Ā h├¼nh b├¼nh h├Ānh, 4 mß║Ęt xung quanh l├Ā 4 h├¼nh chß╗» nhß║Łt.
H├¼nh hß╗Öp chß╗» nhß║Łt
- ─Éß╗ŗnh ngh─®a: H├¼nh hß╗Öp chß╗» nhß║Łt l├Ā h├¼nh hß╗Öp ─æß╗®ng c├│ ─æ├Īy l├Ā h├¼nh chß╗» nhß║Łt.
- T├Łnh chß║źt: H├¼nh hß╗Öp chß╗» nhß║Łt c├│ 6 mß║Ęt l├Ā 6 h├¼nh chß╗» nhß║Łt.
H├¼nh lß║Łp phŲ░ŲĪng
- ─Éß╗ŗnh ngh─®a: H├¼nh lß║Łp phŲ░ŲĪng l├Ā h├¼nh hß╗Öp chß╗» nhß║Łt 2 ─æ├Īy v├Ā 4 mß║Ęt b├¬n ─æß╗üu l├Ā h├¼nh vu├┤ng
- T├Łnh chß║źt: H├¼nh lß║Łp phŲ░ŲĪng c├│ 6 mß║Ęt ─æß╗üu l├Ā h├¼nh vu├┤ng.
H├¼nh ch├│p: L├Ā h├¼nh c├│ ─æ├Īy l├Ā mß╗Öt ─æa gi├Īc v├Ā c├Īc mß║Ęt b├¬n l├Ā c├Īc tam gi├Īc c├│ chung mß╗Öt ─æß╗ēnh.
1.2.2. C├┤ng thŲ░╠üc ti╠ünh th├¬╠ē ti╠üch
Thß╗ā t├Łch khß╗æi ch├│p
\(V=\frac{1}{3}S.h\)
Trong ─æ├│: S l├Ā diß╗ćn t├Łch ─æ├Īy, h l├Ā chiß╗üu cao khß╗æi ch├│p.
Thß╗ā t├Łch khß╗æi l─āng trß╗ź
\(V=B.h\)
Trong ─æ├│: B l├Ā diß╗ćn t├Łch ─æ├Īy, h l├Ā hiß╗üu cao khß╗æi l─āng trß╗ź
Thß╗ā t├Łch khß╗æi hß╗Öp chß╗» nhß║Łt
\( V= abc\)
Trong ─æ├│: a, b, c l├Ā ba k├Łch thŲ░ß╗øc cß╗¦a khß╗æi hß╗Öp chß╗» nhß║Łt.
Thß╗ā t├Łch khß╗æi lß║Łp phŲ░ŲĪng
\( V = a^3\)
Trong ─æ├│ a l├Ā ─æß╗Ö d├Āi cß║Īnh cß╗¦a h├¼nh lß║Łp phŲ░ŲĪng.
1.2.3. Ti╠ē s├┤╠ü th├¬╠ē ti╠üch
Cho khß╗æi ch├│p S.ABC v├Ā A', B', C' l├Ā c├Īc ─æiß╗ām t├╣y ├Į lß║¦n lŲ░ß╗Żt thuß╗Öc SA, SB, SC ta c├│
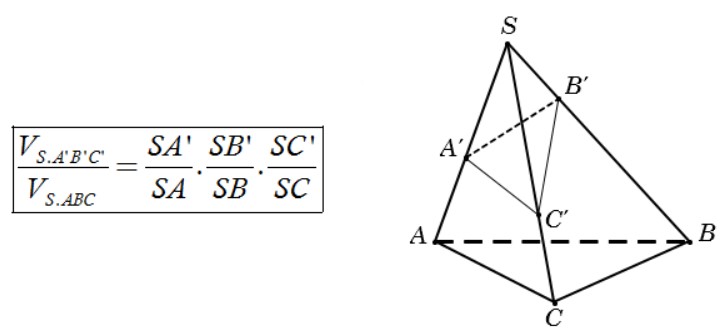
---(─Éß╗ā xem tiß║┐p nß╗Öi dung ─æ├¬╠Ć thi minh hoa╠Ż c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā to├Ān bß╗Ö nß╗Öi dung t├Āi liß╗ću ─Éß╗ü cŲ░ŲĪng ├┤n tß║Łp giß╗»a HK1 m├┤n Toa╠ün 12 n─ām 2023-2024. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Mß╗Øi c├Īc em tham khß║Żo t├Āi liß╗ću c├│ li├¬n quan:
- ─Éß╗ü cŲ░ŲĪng ├┤n tß║Łp giß╗»a HK1 m├┤n Ti├¬╠üng Anh 12 n─ām 2023-2024
- ─Éß╗ü cŲ░ŲĪng ├┤n tß║Łp giß╗»a HK1 m├┤n V├ó╠Żt li╠ü 12 n─ām 2023-2024
- ─Éß╗ü cŲ░ŲĪng ├┤n tß║Łp giß╗»a HK1 m├┤n NgŲ░╠ā V─ān 12 n─ām 2023-2024
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong k├¼ thi sß║»p tß╗øi.
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm







