Tài liệu Đề thi thử tốt nghiệp THPT môn Toán năm 2022-2023 Trường THPT Phú Lâm có đáp án được HOC247 biên tập và tổng hợp và giới thiệu đến các em học sinh lớp 12, với phần đề và đáp án, lời giải chi tiết giúp các em rèn luyện ôn tập chuẩn bị cho kì thi THPT Quốc Gia sắp tới. Hi vọng tài liệu này sẽ có ích cho các em, chúc các em có kết quả học tập tốt!
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG THPT PHÚ LÂM
ĐỀ CHÍNH THỨC |
Năm học: 2022 - 2023 Môn: TOÁN – Khối 12 Thời gian làm bài: 90 phút Ngày kiểm tra: 31/03/2023 |
I. Đề thi
Câu 1: Cho số phức \(z=-1-2\sqrt{6}i\). Phần thực và phần ảo của số phức \(\overline{z}\) là?
A. Phần thực bằng \(-1\) và phần ảo bằng \(2\sqrt{6}\).
B. Phần thực bằng \(-1\) và phần ảo bằng \(2\sqrt{6}i\).
C. Phần thực bằng \(1\) và phần ảo bằng \(2\sqrt{6}\).
D. Phần thực bằng \(-1\) và phần ảo bằng \(-2\sqrt{6}i\).
Câu 2: Đạo hàm của hàm số \(y={{\log }_{2023}}\left( {{x}^{2}}+x \right)\) là
A. \(\frac{2x+1}{{{x}^{2}}+x}\).
B. \(\frac{2x+1}{\left( {{x}^{2}}+x \right).\ln 2023}\).
C. \(\frac{1}{{{x}^{2}}+x}\)
D. \(\frac{1}{\left( {{x}^{2}}+x \right).\ln 2023}\).
Câu 3: Đạo hàm của hàm số \(y={{8}^{x}}\) là
A. \({y}'=\frac{{{8}^{x}}}{\ln 8}\).
B. \({y}'={{8}^{x}}\ln 8\).
C. \({y}'=x{{8}^{x}}\ln 8\).
D. \({y}'=x{{8}^{x-1}}\).
Câu 4: Tìm tập nghiệm \(S\) của bất phương trình \({{5}^{x+1}}-\frac{1}{5}>0\).
A. \(S=\left( -\infty ;\,-2 \right)\).
B. \(S=\left( 1;\,+\infty \right)\).
C. \(S=\left( -1;\,+\infty \right)\).
D. \(S=\left( -2;\,+\infty \right)\).
Câu 5: Cho cấp số cộng có số hạng đầu \(u_1=11\) và công sai d=4. Giá trị của \(u_5\) bằng
A. 2816.
B. 27.
C. 15.
D. - 26.
Câu 6: Trong không gian , cho mặt phẳng . Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng ?
A. \(\vec n = \left( {3; - 2;1} \right)\).
B. \(\vec n = \left( { - 2;1;3} \right)\).
C. \(\vec n = \left( {3;1; - 2} \right)\).
D. \(\vec n = \left( {1; - 2;1} \right)\).
Câu 7: Số giao điểm của đồ thị \((C):y={{x}^{3}}-3{{x}^{2}}+2x+1\) và đường thẳng \(y=1\) là
A. 0.
B. 3.
C. 1.
D. 2.
Câu 8: Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\text{ }\!\![\!\!\text{ }-1;\,2]\) và \(f\left( -1 \right)=2023,\,f\left( 2 \right)=-1. \)
Tích phân \(\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}\)bằng:
A. \(2024. \)
B. \(-2024. \)
C. \(1. \)
D. \(2022. \)
Câu 9: Hàm số nào dưới đây có bảng biến thiên như sau:
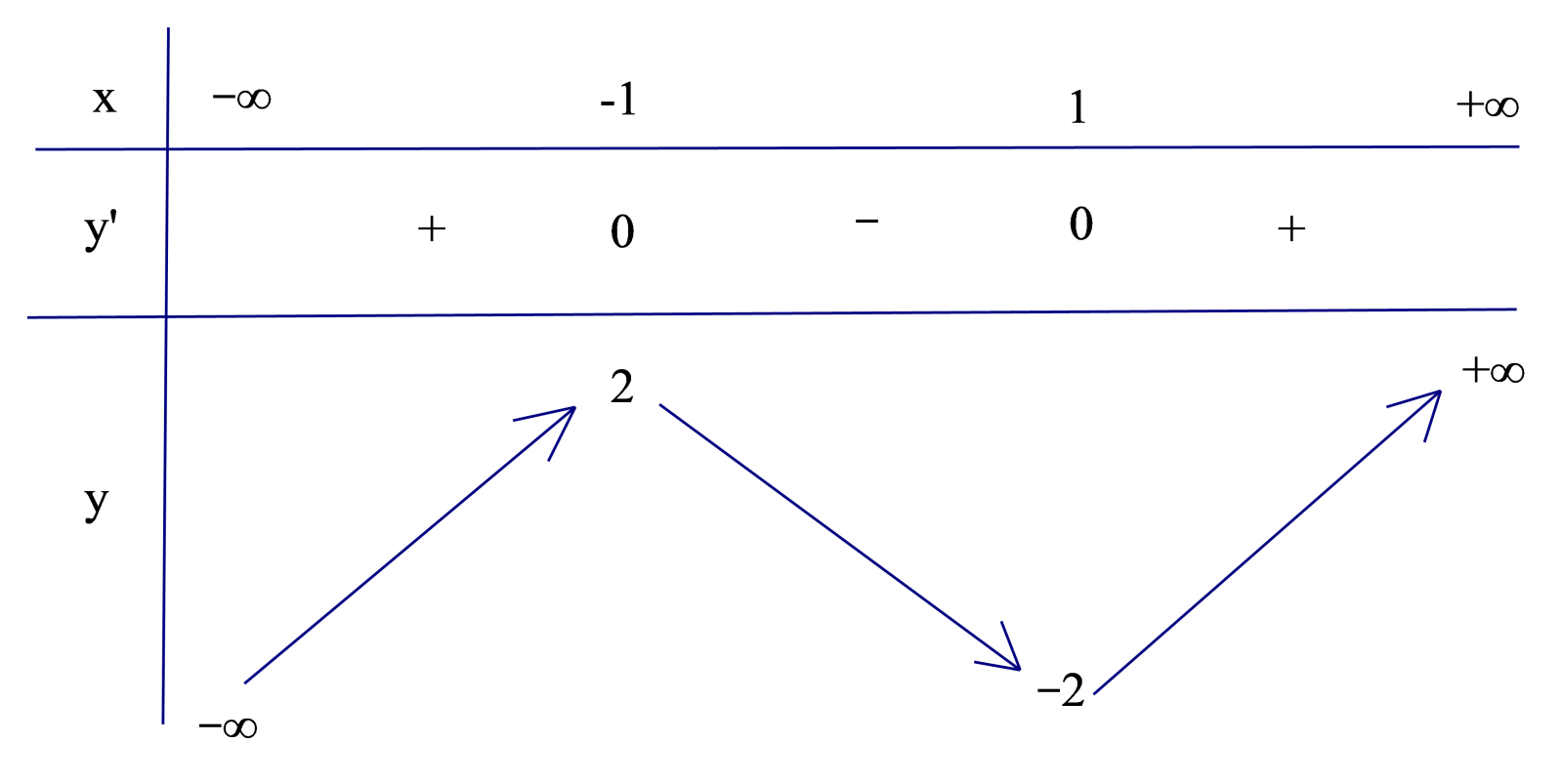
A. \(y={{x}^{4}}-2{{x}^{2}}. \)
B. \(y=-{{x}^{3}}+3x. \)
C. \(y=-{{x}^{4}}+2{{x}^{2}}. \)
D. \(y={{x}^{3}}-3x. \)
Câu 10: Trong không gian \(Oxyz\), mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=25\) có tọa độ tâm \(I\) và bán kính \(R\) là
A. \(I\left( 1;2;3 \right),\,R=5\).
B. \(I\left( 1;-2;3 \right),\,R=5\).
C. \(I\left( 1;2;-3 \right),\,R=25\).
D. \(I\left( 1;2;3 \right),\,R=25\).
Câu 11: Cho điểm \(M\left( 1,-4,-2 \right)\) và mặt phẳng \(\left( P \right):x+y+5z-14=0\). Tính khoảng cách từ \(M\) đến \((P)\).
A. \(2\sqrt{3}\)
B. \(4\sqrt{3}\)
C. \(6\sqrt{3}\)
D. \(3\sqrt{3}\)
Câu 12: Cho số phức \(z\)thỏa mãn \(\left( 1+i \right)z=14-2i\). Tổng phần thực và phần ảo của \(\overline{z}\) bằng
A. \(14. \)
B. \(2. \)
C. \(-2. \)
D. \(-14. \)
Câu 13: Thể tích của khối lăng trụ có diện tích đáy \(S=2{{a}^{2}}\), chiều cao \(h=6a\) là:
A. \(12{{a}^{3}}\).
B. \(4{{a}^{3}}\).
C. \(6{{a}^{3}}\).
D. \(36{{a}^{3}}\).
Câu 14: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA=a\) và \(SA\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABCD\) bằng
A. \(\frac{{{a}^{3}}}{6}\).
B. \(\frac{2{{a}^{3}}}{3}\).
C. \({{a}^{3}}\).
D. \(\frac{{{a}^{3}}}{3}\).
Câu 15: Phương trình tiếp tuyến của đường cong \(y={{x}^{3}}+3{{x}^{2}}-2\) tại điểm có hoành độ \({{x}_{0}}=1\) là
A. \(y=9x+7\).
B. \(y=-9x-7\).
C. \(y=-9x+7\).
D. \(y=9x-7\).
Câu 16 : Trong mặt phẳng Oxy , điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Số phức \(\overline{z}\) là
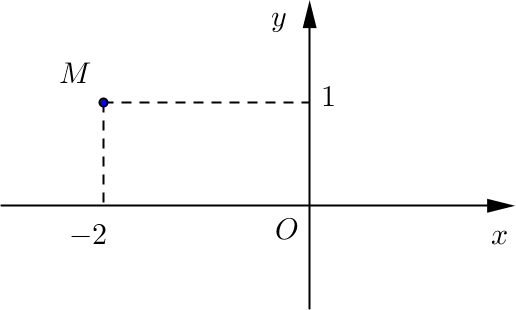
A. \(-2-i\) .
B. \(1-2i\) .
C. \(-2+i\).
D. \(2+i\) .
Câu 17: Cho hình trụ có bán kính đáy \(r\) và độ dài đường sinh \(l\). Diện tích xung quanh \({{S}_{xq}}\) của hình trụ đã cho được tính theo công thức nào dưới đây?
A. \({{S}_{xq}}=4\pi rl\).
B. \({{S}_{xq}}=2\pi rl\).
C. \({{S}_{xq}}=3\pi rl\).
D. \({{S}_{xq}}=\pi rl\).
...
II. Đáp án
HƯỚNG DẪN CHẤM
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
B |
B |
D |
B |
C |
B |
B |
D |
A |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
D |
A |
A |
D |
D |
A |
B |
C |
D |
D |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
B |
A |
A |
A |
B |
D |
A |
D |
B |
D |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
C |
D |
B |
A |
A |
A |
B |
B |
D |
B |
|
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
C |
D |
B |
D |
C |
A |
D |
B |
B |
A |
Câu 1: Cho số phức \(z=-1-2\sqrt{6}i\). Phần thực và phần ảo của số phức \(\overline{z}\) là?
A. Phần thực bằng \(-1\) và phần ảo bằng \(2\sqrt{6}\).
B. Phần thực bằng \(-1\) và phần ảo bằng \(2\sqrt{6}i\).
C. Phần thực bằng \(1\) và phần ảo bằng \(2\sqrt{6}\).
D. Phần thực bằng \(-1\) và phần ảo bằng \(-2\sqrt{6}i\).
Lời giải
Chọn A
\(z=-1-2\sqrt{6}i\Rightarrow \overline{z}=-1+2\sqrt{6}i\)
Vậy \(\overline{z}\)có phần thực bằng \(-1\) và phần ảo bằng \(2\sqrt{6}\).
Câu 2: Đạo hàm của hàm số \(y={{\log }_{2023}}\left( {{x}^{2}}+x \right)\) là
A. \(\frac{2x+1}{{{x}^{2}}+x}\).
B. \(\frac{2x+1}{\left( {{x}^{2}}+x \right).\ln 2023}\).
C. \(\frac{1}{{{x}^{2}}+x}\)
D. \(\frac{1}{\left( {{x}^{2}}+x \right).\ln 2023}\).
Lời giải
Chọn B
Ta có \({y}'={{\left[ {{\log }_{2023}}\left( {{x}^{2}}+x \right) \right]}^{\prime }}=\frac{{{\left( {{x}^{2}}+x \right)}^{\prime }}}{\left( {{x}^{2}}+x \right).\ln 2023}=\frac{2x+1}{\left( {{x}^{2}}+x \right).\ln 2023}\).
Câu 3: Đạo hàm của hàm số \(y={{8}^{x}}\) là
A. \({y}'=\frac{{{8}^{x}}}{\ln 8}\).
B. \({y}'={{8}^{x}}\ln 8\).
C. \({y}'=x{{8}^{x}}\ln 8\).
D. \({y}'=x{{8}^{x-1}}\).
Lời giải
Chọn B
Ta có \({y}'={{\left( {{8}^{x}} \right)}^{\prime }}={{8}^{x}}\ln 8\).
Câu 4: Tìm tập nghiệm \(S\) của bất phương trình \({{5}^{x+1}}-\frac{1}{5}>0\).
A. \(S=\left( -\infty ;\,-2 \right)\).
B. \(S=\left( 1;\,+\infty \right)\).
C. \(S=\left( -1;\,+\infty \right)\).
D. \(S=\left( -2;\,+\infty \right)\).
Lời giải
Chọn D
Bất phương trình tương đương \({{5}^{x+1}}>{{5}^{-1}}\Leftrightarrow x+1>-1\Leftrightarrow x>-2.\)
Câu 5: Cho cấp số cộng có số hạng đầu \(u_1=11\) và công sai d=4. Giá trị của \(u_5\) bằng
A. 2816. B. 27. C. 15. D. - 26.
Lời giải
Chọn B
Ta có : \(\left\{ \begin{array}{l} {u_1} = 11\\ d = 4 \end{array} \right. \Rightarrow {u_5} = {u_1} + 4d = 27\).
Câu 6: Trong không gian , cho mặt phẳng . Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng ?
A. \(\vec n = \left( {3; - 2;1} \right)\).
B. \(\vec n = \left( { - 2;1;3} \right)\).
C. \(\vec n = \left( {3;1; - 2} \right)\).
D. \(\vec n = \left( {1; - 2;1} \right)\).
Lời giải
Chọn C
Từ phương trình mặt phẳng (P) ta có vectơ pháp tuyến của (P) là \(\vec n = \left( {3;1; - 2} \right)\).
Câu 7: Số giao điểm của đồ thị \((C):y={{x}^{3}}-3{{x}^{2}}+2x+1\) và đường thẳng \(y=1\) là
A. 0. B. 3. C. 1. D. 2.
Lời giải
Chọn B
Phương trình hoành độ giao điểm: \({{x}^{3}}-3{{x}^{2}}+2x+1=1\Leftrightarrow {{x}^{3}}-3{{x}^{2}}+2x=0\)
\(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=1 \\ & x=2 \\ \end{align} \right.\).
Vậy có ba giao điểm.
Câu 8: Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\text{ }\!\![\!\!\text{ }-1;\,2]\) và \(f\left( -1 \right)=2023,\,f\left( 2 \right)=-1.\)Tích phân \(\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}\)bằng:
A. \(2024.\) B. \(-2024.\) C. \(1.\) D. \(2022.\)
Lời giải
Chọn B
Ta có: \(\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}=f\left( x \right)\left| \begin{matrix} 2 \\ -1 \\ \end{matrix}\\ =f\left( 2 \right)-f\left( -1 \right)=-1-2023=-2024 \right.\).
Câu 9: Hàm số nào dưới đây có bảng biến thiên như sau:
A. \(y={{x}^{4}}-2{{x}^{2}}.\)
B. \(y=-{{x}^{3}}+3x.\)
C. \(y=-{{x}^{4}}+2{{x}^{2}}.\)
D. \(y={{x}^{3}}-3x.\)
Lời giải
Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với \(a>0.\)
Câu 10: Trong không gian \(Oxyz\), mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=25\) có tọa độ tâm \(I\) và bán kính \(R\) là
A. \(I\left( 1;2;3 \right),\,R=5\).
B. \(I\left( 1;-2;3 \right),\,R=5\).
C. \(I\left( 1;2;-3 \right),\,R=25\).
D. \(I\left( 1;2;3 \right),\,R=25\).
Lời giải
Chọn A
Ta có, tọa độ tâm: \(I\left( 1;2;3 \right)\)
Bán kính: \(R=\sqrt{25}=5\)
...
---(Để xem đầy đủ nội dung đề thi và đáp án chi tiết, các em vui lòng xem online hoặc đăng nhập để tải về máy)---
Trên đây là một phần trích đoạn nội dung Đề thi thử tốt nghiệp THPT môn Toán năm 2022-2023 Trường THPT Phú Lâm có đáp án. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Chúc các em học tập tốt!
