HOC247 xin giß╗øi thiß╗ću ─Éß╗ü thi thß╗Ł tß╗æt nghiß╗ćp THPT m├┤n To├Īn n─ām 2022-2023 TrŲ░ß╗Øng THPT Huyß╗ćn Mß╗╣ Lß╗Öc - Vß╗ź Bß║Żn c├│ ─æ├Īp ├Īn ─æß╗ā c├Īc em c├│ nhiß╗üu nguß╗ōn tŲ░ liß╗ću ├┤n tß║Łp cho kß╗│ thi quan trß╗Źng sß║»p tß╗øi. ─Éß╗ü thi bao gß╗ōm 50 c├óu hß╗Åi trß║»c nghiß╗ćm v├Ā bß║Żng ─æ├Īp ├Īn gi├║p c├Īc em dß╗ģ d├Āng ─æß╗æi chiß║┐u. Ch├║c c├Īc em chuß║®n bß╗ŗ cho kß╗│ thi thß║Łt tß╗æt v├Ā ─æß║Īt ─æŲ░ß╗Żc kß║┐t quß║Ż cao trong hß╗Źc tß║Łp.
|
Sß╗× GI├üO Dß╗żC V├Ć ─É├ĆO Tß║ĀO TRŲ»ß╗£NG THPT Mß╗Ė Lß╗śC |
─Éß╗Ć THI THß╗¼ Tß╗ÉT NGHIß╗åP THPT N─éM 2023 M├öN TO├üN Thß╗Øi gian l├Ām b├Āi: 90 ph├║t |
Hß╗Ź, t├¬n th├Ł sinh:................................................................................
Sß╗æ b├Īo danh:.....................................................................................
1. Đề thi
C├óu 1: Biß║┐t \(\int\limits_{1}^{2}{f\left( x \right)}\,dx=2\) v├Ā \(\int\limits_{1}^{5}{f\left( x \right)}\,dx=5\), khi ─æ├│ \(\int\limits_{2}^{5}{f\left( x \right)dx}\) bß║▒ng
A.\(3.\)
B. \(7.\)
C. \(10.\)
D. \(-3.\)
C├óu 2: Cho khß╗æi ch├│p c├│ thß╗ā t├Łch \(4{{a}^{3}}\) v├Ā diß╗ćn t├Łch ─æ├Īy \(4{{a}^{2}}.\) Chiß╗üu cao cß╗¦a khß╗æi ch├│p ─æ├Ż cho bß║▒ng
A. \(a.\)
B. \(2a.\)
C. \(3a.\)
D. \(4a.\)
C├óu 3: Cho h├¼nh phß║│ng giß╗øi hß║Īn bß╗¤i ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=\sin x\), trß╗źc \(Ox\) v├Ā c├Īc ─æŲ░ß╗Øng thß║│ng \(x=0,x=\pi \) quay xung quanh \(Ox.\) Thß╗ā t├Łch khß╗æi tr├▓n xoay tß║Īo th├Ānh bß║▒ng
A. \(\int\limits_{0}^{\pi }{\sin }x\,dx.\)
B. \(\int\limits_{0}^{\pi }{{{\sin }^{2}}}x\,dx.\)
C. \(\pi \int\limits_{0}^{\pi }{{{\sin }^{2}}}x\,dx.\)
D. \(\pi \int\limits_{0}^{\pi }{{{\cos }^{2}}}x\,dx.\)
C├óu 4: Nguy├¬n h├Ām cß╗¦a h├Ām sß╗æ \(f\left( x \right)=4x+\sin x\) l├Ā
A. \(4-\cos x+C.\)
B. \(2{{x}^{2}}+\cos x+C.\)
C. \(2{{x}^{2}}-\cos x+C.\)
D. \(4+\cos x+C.\)
C├óu 5: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau
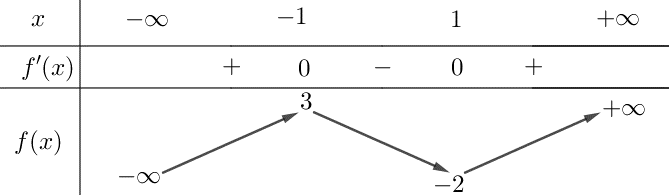
H├Ām sß╗æ ─æ├Ż cho ─æß╗ōng biß║┐n tr├¬n khoß║Żng n├Āo dŲ░ß╗øi ─æ├óy?
A. \(\left( -\infty ;3 \right).\)
B. \(\left( -2;+\infty \right).\)
C. \(\left( -\infty ;-1 \right).\)
D. \(\left( -1;1 \right).\)
C├óu 6: Trong kh├┤ng gian \(Oxyz,\) cho mß║Ęt cß║¦u \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z-5=0.\) T├óm cß╗¦a mß║Ęt cß║¦u \(\left( S \right)\) c├│ tß╗Źa ─æß╗Ö l├Ā
A. \(\left( -2;4;-6 \right).\)
B. \(\left( -1;2;-3 \right).\)
C. \(\left( 2;-4;6 \right).\)
D. \(\left( 1;-2;3 \right).\)
C├óu 7: Trong kh├┤ng gian \(Oxyz,\) cho \(\vec{a}=\left( 1;-2;3 \right)\) v├Ā \(\vec{b}=\left( -1;3;0 \right)\). VectŲĪ \(\vec{a}-\vec{b}\) c├│ tß╗Źa ─æß╗Ö l├Ā
A. \(\left( -2;5;-3 \right).\)
B. \(\left( 2;-5;3 \right).\)
C. \(\left( 0;1;3 \right).\)
D. \(\left( 2;-5;-3 \right).\)
C├óu 8: Cho khß╗æi l─āng trß╗ź tam gi├Īc c├│ chiß╗üu cao \(h=3\) v├Ā ─æ├Īy l├Ā tam gi├Īc ─æß╗üu cß║Īnh \(a=2.\) Thß╗ā t├Łch khß╗æi l─āng trß╗ź ─æ├Ż cho bß║▒ng
A. \(3\sqrt{3}.\)
B. \(6\sqrt{3}.\)
C. \(6.\)
D. \(9\sqrt{3}.\)
C├óu 9: Mß╗Öt cß║źp sß╗æ cß╗Öng c├│ hai sß╗æ hß║Īng li├¬n tiß║┐p l├Ā \(-6\) v├Ā \(4.\) Sß╗æ hß║Īng tiß║┐p theo cß╗¦a cß║źp sß╗æ cß╗Öng l├Ā
A. \(-2.\)
B. \(10.\)
C. \(14.\)
D. \(2.\)
C├óu 10: Cho h├¼nh trß╗ź c├│ b├Īn k├Łnh ─æ├Īy \(r=3\) v├Ā ─æß╗Ö d├Āi ─æŲ░ß╗Øng sinh \(l=5.\) Diß╗ćn t├Łch xung quanh cß╗¦a h├¼nh trß╗ź ─æ├Ż cho bß║▒ng
A. \(30\pi .\)
B. \(15\pi .\)
C. \(45\pi .\)
D. \(24\pi .\)
C├óu 11: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ saU
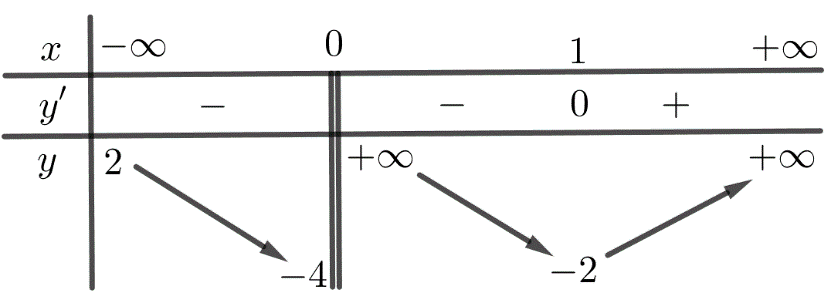
Tiß╗ćm cß║Łn ngang cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ l├Ā
A. \(x=0.\)
B. \(y=2.\)
C. \(y=0.\)
D. \(x=2.\)
C├óu 12: Tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh \({{\log }_{0,5}}x+2\ge 0\) l├Ā
A. \(\left( -\infty ;4 \right].\)
B. \(\left( 0;+\infty \right).\)
C. \(\left( 0;4 \right].\)
D. \(\left( 0;4 \right).\)
C├óu 13: H├Ām sß╗æ n├Āo dŲ░ß╗øi ─æ├óy c├│ bß║Żng biß║┐n thi├¬n nhŲ░ h├¼nh sau
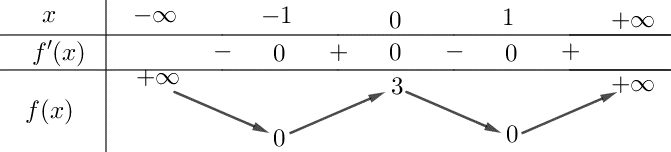
A. \(y=3{{x}^{4}}-6{{x}^{2}}+3.\)
B. \(y=-{{x}^{3}}+3x+3.\)
C. \(y={{x}^{4}}-2{{x}^{2}}+3.\)
D. \(y=-{{x}^{4}}-2{{x}^{2}}+3.\)
C├óu 14. Cho sß╗æ thß╗▒c \(a\) thß╗Åa m├Żn \({{a}^{3}}>{{a}^{\pi }}\). Mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy ─æ├║ng?
A. \(0 < a < 1\).
B. \(a<1.\).
C. \(a>1\).
D. \(a=1\).
|
C├óu 15: Cho h├Ām sß╗æ \(y=f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\) c├│ ─æß╗ō thß╗ŗ nhŲ░ h├¼nh vß║Į b├¬n. Sß╗æ gi├Ī trß╗ŗ nguy├¬n dŲ░ŲĪng cß╗¦a tham sß╗æ \(m\) ─æß╗ā phŲ░ŲĪng tr├¼nh \(f\left( x \right)=m\) c├│ hai nghiß╗ćm ph├ón biß╗ćt l├Ā
A. \(0.\) B. \(1.\) C. \(2.\) D. \(3.\) |
C├óu 16: Tß║Łp x├Īc ─æß╗ŗnh cß╗¦a h├Ām sß╗æ \(y={{\left( 9-{{x}^{2}} \right)}^{\frac{1}{3}}}+{{\left( x-2 \right)}^{-2}}\) l├Ā
A. \(D=\mathbb{R}\backslash \left\{ 2 \right\}.\)
B. \(D=\left( -3;2 \right)\cup \left( 2;3 \right).\)
C. \(D=\left[ -3;3 \right]\backslash \left\{ 2 \right\}.\)
D. \(D=\left( -3;3 \right).\)
C├óu 17: Vß╗øi \(a,b\) l├Ā c├Īc sß╗æ thß╗▒c dŲ░ŲĪng t├╣y ├Į thß╗Åa m├Żn \({{\log }_{3}}b-2{{\log }_{9}}a=2.\)Mß╗ćnh ─æß╗ü n├Āo dŲ░ß╗øi ─æ├óy ─æ├║ng?
A. \(a=27b.\)
B. \(a=9b.\)
C. \(b-a=9.\)
D. \(b=9a.\)
...
2. ─É├Īp ├Īn
Lß╗£I GIß║óI CHI TIß║ŠT
C├óu 1: Biß║┐t \(\int\limits_{1}^{2}{f\left( x \right)}\,dx=2\) v├Ā \(\int\limits_{1}^{5}{f\left( x \right)}\,dx=5\), khi ─æ├│ \(\int\limits_{2}^{5}{f\left( x \right)dx}\) bß║▒ng
A. \(3.\) B. \(7.\) C. \(10.\) D. \(-3.\)
Lß╗Øi giß║Żi
Ta c├│ \(\int\limits_{1}^{5}{f\left( x \right)\text{d}x}=\int\limits_{1}^{2}{f\left( x \right)\text{d}x}+\int\limits_{2}^{5}{f\left( x \right)\text{d}x}\Rightarrow 5=2+\int\limits_{2}^{5}{f\left( x \right)dx}\Rightarrow \int\limits_{2}^{5}{f\left( x \right)dx}=3.\)
C├óu 2: Cho khß╗æi ch├│p c├│ thß╗ā t├Łch \(4{{a}^{3}}\) v├Ā diß╗ćn t├Łch ─æ├Īy \(4{{a}^{2}}.\) Chiß╗üu cao cß╗¦a khß╗æi ch├│p ─æ├Ż cho bß║▒ng
A. \(a.\) B. \(2a.\) C. \(3a.\) D. \(4a.\)
Lß╗Øi giß║Żi
Ta c├│ \(V=\frac{1}{3}h.S\Rightarrow \frac{1}{3}.h.4{{a}^{2}}=4{{a}^{3}}\Rightarrow h=3a.\) Chß╗Źn C.
C├óu 3: Cho h├¼nh phß║│ng giß╗øi hß║Īn bß╗¤i ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=\sin x\), trß╗źc \(Ox\) v├Ā c├Īc ─æŲ░ß╗Øng thß║│ng \(x=0,x=\pi \) quay xung quanh \(Ox.\) Thß╗ā t├Łch khß╗æi tr├▓n xoay tß║Īo th├Ānh bß║▒ng
A. \(\int\limits_{0}^{\pi }{\sin }x\,dx.\) B. \(\int\limits_{0}^{\pi }{{{\sin }^{2}}}x\,dx.\) C. \(\pi \int\limits_{0}^{\pi }{{{\sin }^{2}}}x\,dx.\) D. \(\pi \int\limits_{0}^{\pi }{{{\cos }^{2}}}x\,dx.\)
Lß╗Øi giß║Żi
Ta c├│ \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}}\left( x \right)dx=\pi \int\limits_{0}^{\pi }{{{\sin }^{2}}x\,}dx.\) Chß╗Źn C.
C├óu 4: Nguy├¬n h├Ām cß╗¦a h├Ām sß╗æ \(f\left( x \right)=4x+\sin x\) l├Ā
A. \(4-\cos x+C.\) B. \(2{{x}^{2}}+\cos x+C.\) C. \(2{{x}^{2}}-\cos x+C.\) D. \(4+\cos x+C.\)
Lß╗Øi giß║Żi
Ta c├│ \(\int{f\left( x \right)}\,dx=\int{\left( 4x+\sin x \right)}\,dx=2{{x}^{2}}-\cos x+C.\) Chß╗Źn C.
C├óu 5: Cho h├Ām sß╗æ \(y=f\left( x \right)\) c├│ bß║Żng biß║┐n thi├¬n nhŲ░ sau

H├Ām sß╗æ ─æ├Ż cho ─æß╗ōng biß║┐n tr├¬n khoß║Żng n├Āo dŲ░ß╗øi ─æ├óy?
A. \(\left( -\infty ;3 \right).\) B. \(\left( -2;+\infty \right).\) C. \(\left( -\infty ;-1 \right).\) D. \(\left( -1;1 \right).\)
C├óu 6: Trong kh├┤ng gian \(Oxyz,\) cho mß║Ęt cß║¦u \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z-5=0.\) T├óm cß╗¦a mß║Ęt cß║¦u \(\left( S \right)\) c├│ tß╗Źa ─æß╗Ö l├Ā
A. \(\left( -2;4;-6 \right).\) B. \(\left( -1;2;-3 \right).\) C. \(\left( 2;-4;6 \right).\) D. \(\left( 1;-2;3 \right).\)
Lß╗Øi giß║Żi
Ta c├│ \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z-5=0\)
\(\Rightarrow \left\{ \begin{align} & a=1 \\ & b=-2 \\ & c=3 \\ & d=-5 \\ \end{align} \right.\)
\(\Rightarrow I\left( 1;-2;3 \right).\) Chß╗Źn D.
C├óu 7: Trong kh├┤ng gian \(Oxyz,\) cho \(\vec{a}=\left( 1;-2;3 \right)\) v├Ā \(\vec{b}=\left( -1;3;0 \right)\). VectŲĪ \(\vec{a}-\vec{b}\) c├│ tß╗Źa ─æß╗Ö l├Ā
A. \(\left( -2;5;-3 \right).\) B. \(\left( 2;-5;3 \right).\) C. \(\left( 0;1;3 \right).\) D. \(\left( 2;-5;-3 \right).\)
Lß╗Øi giß║Żi
C├│ \(\vec{c}=\vec{a}-\vec{b}=\left( 1;-2;3 \right)-\left( -1;3;0 \right)=\left( 2;-5;3 \right).\) Chß╗Źn B.
C├óu 8: Cho khß╗æi l─āng trß╗ź tam gi├Īc c├│ chiß╗üu cao \(h=3\) v├Ā ─æ├Īy l├Ā tam gi├Īc ─æß╗üu cß║Īnh \(a=2.\) Thß╗ā t├Łch khß╗æi l─āng trß╗ź ─æ├Ż cho bß║▒ng
A. \(3\sqrt{3}.\) B. \(6\sqrt{3}.\) C. \(6.\) D. \(9\sqrt{3}.\)
Lß╗Øi giß║Żi
Ta c├│ \(V=h.S=3.\frac{{{2}^{2}}\sqrt{3}}{4}=3\sqrt{3}.\) Chß╗Źn A.
C├óu 9: Mß╗Öt cß║źp sß╗æ cß╗Öng c├│ hai sß╗æ hß║Īng li├¬n tiß║┐p l├Ā \(-6\) v├Ā \(4.\) Sß╗æ hß║Īng tiß║┐p theo cß╗¦a cß║źp sß╗æ cß╗Öng l├Ā
A. \(-2.\) B. \(10.\) C. \(14.\) D. \(2.\)
Lß╗Øi giß║Żi
C├┤ng sai: \(d=4-\left( -6 \right)=10.\) Do ─æ├│ sß╗æ hß║Īng tiß║┐p theo l├Ā \(4+d=14.\) Chß╗Źn C.
C├óu 10: Cho h├¼nh trß╗ź c├│ b├Īn k├Łnh ─æ├Īy \(r=3\) v├Ā ─æß╗Ö d├Āi ─æŲ░ß╗Øng sinh \(l=5.\) Diß╗ćn t├Łch xung quanh cß╗¦a h├¼nh trß╗ź ─æ├Ż cho bß║▒ng
A. \(30\pi .\) B. \(15\pi .\) C. \(45\pi .\) D. \(24\pi .\)
Lß╗Øi giß║Żi
Diß╗ćn t├Łch xung quanh cß╗¦a h├¼nh trß╗ź \({{S}_{xq}}=2\pi rl=2\pi .3.5=30\pi .\) Chß╗Źn A.
..
---(─Éß╗ā xem ─æß║¦y ─æß╗¦ nß╗Öi dung ─æß╗ü thi v├Ā ─æ├Īp ├Īn chi tiß║┐t, c├Īc em vui l├▓ng xem online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch ─æoß║Īn nß╗Öi dung ─Éß╗ü thi thß╗Ł tß╗æt nghiß╗ćp THPT m├┤n To├Īn n─ām 2022-2023 TrŲ░ß╗Øng THPT Huyß╗ćn Mß╗╣ Lß╗Öc - Vß╗ź Bß║Żn c├│ ─æ├Īp ├Īn. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt!
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm