Mời các em cùng tham khảo Đề thi thử tốt nghiệp THPT môn Toán năm 2022-2023 Trường THPT Đào Sơn Tây có đáp án do HOC247 sưu tầm và biên soạn nhằm giúp cho các em học sinh lớp 12 trong quá trình ôn thi để học tập chủ động hơn, nắm bắt các kiến thức tổng quan về môn học và chuẩn bị tốt cho kì thi tốt nghiệp sắp tới. Hi vọng tài liệu này sẽ là người bạn đồng hành, giúp các em đạt kết quả cao trong học tập.
|
TRƯỜNG THPT ĐÀO SƠN TÂY TỔ TOÁN ĐỀ MINH HỌA (Đề này có 1 trang) |
ÔN THI TỐT NGHIỆP THPT NĂM HỌC 2022 - 2023 Môn: TOÁN - Lớp 12 - Chương trình chuẩn Thời gian: 90 phút (Không kể thời gian phát đề)
|
|
|
Họ và tên thí sinh: ............................................................................. SBD: .................... |
Mã đề thi 123 |
|
1. Đề thi
Câu 1. Trong không gian, cho tam giác \(ABC\)đều cạnh\(2a.\) Gọi \(M\) là trung điếm của\(BC.\) Khi quay tam giác \(ABC\) xung quanh trục \(AM\)thì đường gấp khúc \(ABC\) tạo thành một hình nón. Tính diện tích xung quanh của hình nón đó
A. \({{S}_{xq}}=2\pi {{a}^{2}}\).
B. \({{S}_{xq}}=4\pi {{a}^{2}}\).
C. \({{S}_{xq}}=6\pi {{a}^{2}}\).
D. \({{S}_{xq}}=8\pi {{a}^{2}}\).
Câu 2. Thể tích của khối chóp có đáy là tam giác đều cạnh \(a\) và chiều cao \(4a\) bẳng
A. \({{a}^{3}}\sqrt{3}\).
B. \(4{{a}^{3}}\).
C. \(\frac{{{a}^{3}}\sqrt{3}}{3}\).
D. \(\frac{4}{3}{{a}^{3}}\).
Câu 3. Họ các nguyên hàm của hàm số \(f(x)={{\text{e}}^{2x+3}}\) là
A. \(\int{f}(x)\text{d}x=\frac{1}{3}{{\text{e}}^{2x+3}}+C\).
B. \(\int{f}(x)\text{d}x=\frac{1}{2}{{\text{e}}^{2x+3}}+C\).
C. \(\int{f}(x)\text{d}x={{\text{e}}^{2x+3}}+C\).
D. \(\int{f}(x)\text{d}x=2{{\text{e}}^{2+3}}+C\).
Câu 4. Tập xác định của hàm số \(y={{\left( x+2 \right)}^{\frac{3}{4}}}\) là
A. \(\left( -2;+\infty \right)\).
B. \(\left[ -2;+\infty \right)\).
C. \(\mathbb{R}\).
D. \(\left( 0;+\infty \right)\).
Câu 5. Trong không gian \(Oxyz\), vectơ \(\vec{n}=\left( 1;-1;-3 \right)\) là một vectơ pháp tuyến của mặt phẳng nào sau đây ?
A. \(x+y-3z-3=0\).
B. \(x-y+3z-3=0\).
C. \(x-y-3z-3=0\).
D. \(x-3z-3=0\).
Câu 6. Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
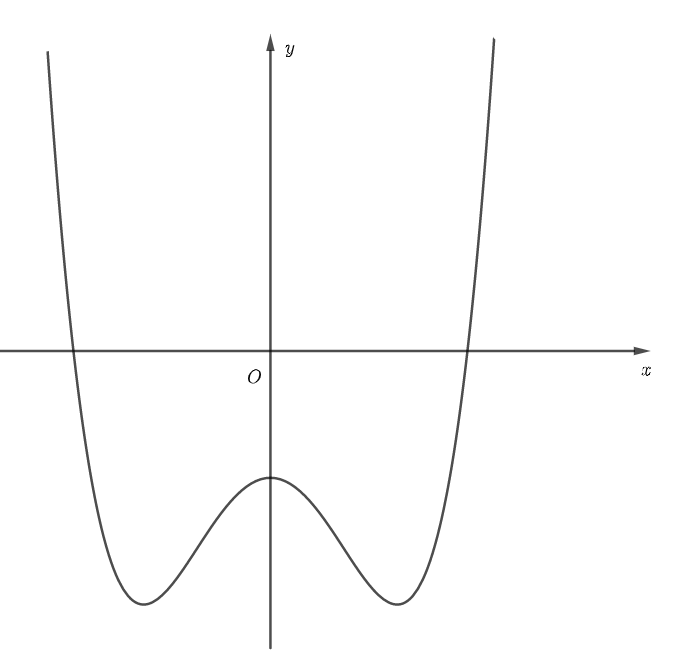
A. \(y=\frac{2x+1}{x-1}\).
B. \(y={{x}^{4}}-2{{x}^{2}}-1\).
C. \(y={{x}^{3}}-2{{x}^{2}}-1\).
D. \(y=-{{x}^{2}}+2x-1\).
Câu 7. Trong không gian \(Oxyz\), cho hai vec tơ \(\vec{u}=\left( 1;1;0 \right)\) và \(\vec{v}=\left( 2;0;-1 \right)\). Tính độ dài \(\left| \vec{u}+2\vec{v} \right|\).
A. \(2\).
B. \(2\sqrt{2}\).
C. \(\sqrt{30}\).
D. \(\sqrt{22}\).
Câu 8. Cho khối lăng trụ có diện tích đáy \(B=5\) và chiều cao \(h=6\). Thể tích của khối lăng trụ đã cho bằng
A. \(15\).
B. \(10\).
C. \(180\).
D. \(30\).
Câu 9. Tập nghiệm của bất phương trình\({{\log }_{3}}x<2\) là
A. \(\left( 0;9 \right)\).
B. \(\left( 0;+\infty \right)\).
C. \(\left( 9;+\infty \right)\).
D. \(\left( -\infty ;9 \right)\).
Câu 10. Nếu \(\int_{0}^{1}{f}(x)\text{d}x=3\) và \(\int_{0}^{3}{f}(x)\text{d}x=-2\) thì \(\int_{1}^{3}{f}(x)\text{d}x\) bằng
A. \(-6\).
B. \(-5\).
C. \(5\).
D. \(1\).
Câu 11. Với \(n\) là số nguyên dương bất kỳ, \(n\ge 3\), công thức nào sau đây đúng?
A. \(A_{n}^{3}=\frac{n!}{3!(n-3)!}\).
B. \(A_{n}^{3}=\frac{n!}{(n-3)!}\).
C. \(A_{n}^{3}=\frac{(n-3)!}{n!}\).
D. \(A_{n}^{3}=\frac{3!(n-3)!}{n!}\).
Câu 12. Phương trình \(\log \left( 4x+1 \right)=\log \left( 2x+5 \right)\) có nghiệm là
A. \(x=2\).
B. \(x=1\).
C. \(x=3\).
D. \(x=-1\).
Câu 13. Diện tích \(S\) của mặt cầu bán kính \(r\) được tính theo công thức nào dưới đây?
A. \(S=\pi {{r}^{2}}\).
B. \(S=4\pi {{r}^{2}}\).
C. \(S=2\pi {{r}^{2}}\).
D. \(S=\frac{4}{3}\pi {{r}^{2}}\).
Câu 14. Trong không gian \(Oxyz,\) cho mặt cầu \((S)\) có phương trình \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y+2z-4=0\) và đi qua điểm \(M(1;1;0)~\). Mặt phẳng nào dưới đây tiếp xúc với mặt cầu \(\left( S \right)\)tại\(M\)?
A. \(3y+z-3=0\).
B. \(2x+3y+z-5=0\).
C. \(3y+z-2=0\).
D. \(2x+3y+z+5=0\).
Câu 15. Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=2\) và công sai \(d=5.\) Giá trị của \({{u}_{4}}\) bằng
A. \(17\).
B. \(250\).
C. \(12\).
D. \(22\).
Câu 16. Nếu \(\int\limits_{0}^{1}{\left[ f(x)+2x \right]dx=2}\) thì \(\int_{0}^{1}{f}(x)dx\) bằng
A. \(4\).
B. \(2\).
C. \(0\).
D. \(1\).
...
2. Đáp án
|
HƯỚNG DẪN GIẢI - ĐÁP ÁN CHI TIẾT |
Mã đề thi 123 |
Câu 1.
Lời giải
Chọn A
Hình nón có bán kình đáy \(r=a\), đường sinh \(l=AB=2a\). Suy ra: \({{S}_{xq}}=\pi rl=2\pi {{a}^{2}}\).
Câu 2.
Lời giải
Chọn C
Diện tích đáy \(B=\frac{{{a}^{2}}\sqrt{3}}{4}\), suy ra: \(V=\frac{1}{3}Bh=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.4a=\frac{{{a}^{3}}\sqrt{3}}{3}\).
Câu 3.
Lời giải
Chọn B
Ta có: \(\int{f\left( x \right)\text{d}x}=\int{{{\text{e}}^{2x+3}}\text{d}x}=\frac{1}{2}{{\text{e}}^{2x+3}}+C\).
Câu 4.
Lời giải
Chọn A
Ta có \(x+2>0\)\(\Leftrightarrow x>-2\).
Câu 5.
Lời giải
Chọn C
Câu 6.
Lời giải
Chọn B
Đồ thị là của hàm số trùng phương có hệ số bậc bốn dương.
Câu 7.
Lời giải
Chọn C
Ta có \(\overrightarrow{u}+2\overrightarrow{v}=\left( 5;1;-2 \right)\)\(\Rightarrow \left| \overrightarrow{u}+2\overrightarrow{v} \right|=\sqrt{30}\).
Câu 8.
Lời giải
Chọn D
Ta có \(V=Vh=5.6=30\).
Câu 9.
Lời giải
Chọn A
Ta có: \({{\log }_{3}}x<2\)\(\Leftrightarrow \left\{ \begin{align} & x>0 \\ & x<{{3}^{2}} \\ \end{align} \right.\Leftrightarrow 0 < x < 9\)
Câu 10.
Lời giải
Chọn B
Ta có: \(\int_{1}^{3}{f}(x)\text{d}x\)\(=\int_{0}^{3}{f}(x)\text{d}x-\int_{0}^{1}{f}(x)\text{d}x=-2-3=-5\)
Câu 11.
Lời giải
Chọn B
Câu 12.
Lời giải
Chọn A
Ta có \(\log \left( 4x+1 \right)=\log \left( 2x+5 \right)\)
\(\Leftrightarrow \left\{ \begin{align} & 4x+1>0 \\ & 4x+1=2x+5 \\ \end{align} \right.\)
\(\Leftrightarrow \left\{ \begin{align} & x>-\frac{1}{4} \\ & x=2 \\ \end{align} \right.\Leftrightarrow x=2\).
Câu 13.
Lời giải
Chọn B
Câu 14.
Lời giải
Chọn A
Mặt cầu có tâm \(I\left( 1;-2;-1 \right)\), bán kính \(R=\sqrt{10}\).
Mặt phẳng tiếp xúc với mặt cầu tại \(M\) có véc-tơ pháp tuyến là \(\overrightarrow{n}=\overrightarrow{IM}=\left( 0;3;1 \right)\).
...
---(Để xem đầy đủ nội dung đề thi và đáp án chi tiết, các em vui lòng xem online hoặc đăng nhập để tải về máy)---
Trên đây là một phần trích đoạn nội dung Đề thi thử tốt nghiệp THPT môn Toán năm 2022-2023 Trường THPT Đào Sơn Tây có đáp án. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Chúc các em học tập tốt!













