Để giúp các em học sinh có thêm tài liệu học tập, rèn luyện kĩ năng làm đề, kết hợp củng cố kiến thức chuẩn bị bước vào kì thi HK2 lớp 12 sắp tới. HOC247 xin giới thiệu Đề cương ôn tập HK2 môn Toán 12 năm 2022-2023. Mời các em cùng quý thầy cô tham khảo đề thi dưới đây. Chúc các em đạt được nhiều điểm 10 trong kỳ thi sắp đến!
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG THPT NGUYỄN THƯỢNG HIỀN |
ĐỀ CƯƠNG ÔN TẬP THI HỌC KÌ 2 NĂM HỌC 2022-2023 MÔN TOÁN 12 |
A. Nội dung, phạm vi kiểm tra
|
Phân môn |
Chương trình từ đầu học kì II đến hết bài |
|
Giải tích |
Cộng, trừ, nhân số phức |
|
Hình học |
Phương trình đường thẳng |
B. Kiến thức trọng tâm
I. NGUYÊN HÀM
1. Tính chất
\(\int{f'(x)dx}=f(x)+C\)
\(\int{kf\left( x \right)d\text{x}}=k\int{f\left( x \right)d\text{x}}\)
\(\int{\left[ f\left( x \right)\pm g\left( x \right) \right]d\text{x}}=\int{f\left( x \right)d\text{x}}\pm \int{g\left( x \right)d\text{x}}\)
2. Bảng nguyên hàm các hàm số thường gặp
|
\(\int{0dx=C}\) 2. \(\int{dx=x+C}\) |
|
|
\(\int{{{x}^{\alpha }}dx=\frac{1}{\alpha +1}{{x}^{\alpha +1}}+C}\left( \alpha \ne -1 \right)\) |
\(\int{{{\left( ax+b \right)}^{\alpha }}\operatorname{dx}}=\frac{1}{a}\frac{{{\left( ax+b \right)}^{\alpha +1}}}{\alpha +1}+c\,,\alpha \ne -1\) |
|
\(\int{\frac{1}{{{x}^{2}}}dx=-\frac{1}{x}+C}\) |
\(\int{xdx=\frac{{{x}^{2}}}{2}+C}\) |
|
\(\int{\frac{1}{x}dx=\ln \left| x \right|+C}\) |
\(\int{\frac{\operatorname{dx}}{ax+b}}=\frac{1}{a}\ln \left| ax+b \right|+c\) |
|
\(\int{{{e}^{x}}dx={{e}^{x}}+C}\) |
\(\int{{{e}^{ax+b}}dx=\frac{1}{a}{{e}^{ax+b}}+C}\) |
|
\(\int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}\) |
\(\int{{{a}^{kx+b}}dx=\frac{1}{k}\frac{{{a}^{kx+b}}}{\ln a}+C}\) |
|
\(\int{\cos xdx=\sin x+C}\) |
\(\int{\cos \left( ax+b \right)dx=\frac{1}{a}\sin \left( ax+b \right)+C}\) |
|
\(\int{sinxdx=-co\operatorname{s}x+C}\) |
\(\int{\sin \left( ax+b \right)dx=-\frac{1}{a}\cos \left( ax+b \right)+C}\) |
|
\(\int{\tan x.dx\,=-\ln |\cos x|+C}\) |
\(\int{\frac{1}{{{\cos }^{2}}\left( ax+b \right)}dx=\frac{1}{a}\tan \left( ax+b \right)+C}\) |
|
\(\int{\cot x.dx\,=\ln |\sin x|+C}\) |
\(\int{\frac{1}{{{\sin }^{2}}\left( ax+b \right)}dx=-\frac{1}{a}\cot \left( ax+b \right)+C}\) |
|
\(\int{\frac{1}{{{\cos }^{2}}x}dx=\tan x+C}\) |
|
|
\(\int{\frac{1}{{{\sin }^{2}}x}dx=-\cot x+C}\) |
|
...
II. TÍCH PHÂN
III. SỐ PHỨC
IV. PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
...
C. Ma trận đề kiểm tra
|
TT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ nhận thức |
Tổng |
||||||
|
NB |
TH |
VD (TL) |
VDC (TL) |
Số CH |
% tổng điểm |
|||||
|
TN |
TL |
|||||||||
|
1 |
Nguyên hàm-Tích phân-Ứng dụng của tích phân |
1.1 Nguyên hàm |
2 |
3 |
1 |
1 |
15 |
3 |
70 |
|
|
1.2 Tích phân |
3 |
2 |
||||||||
|
1.3 Ứng dụng của tích phân trong hình hoc |
3 |
2 |
||||||||
|
2 |
Số phức |
2.1 Số phức |
3 |
2 |
1 |
10 |
||||
|
2.2 Cộng, trừ và nhân số phức |
3 |
2 |
||||||||
|
3 |
Phương pháp tọa độ trong không gian |
3.1 Hệ tọa độ trong không gian |
1 |
1 |
1 |
|
10 |
1 |
30 |
|
|
3.2 Phương trình mặt phẳng |
2 |
2 |
||||||||
|
3.3 Phương trình đường thẳng |
3 |
1 |
||||||||
|
Tổng |
20 |
15 |
2 |
2 |
35 |
4 |
100 |
|||
|
Tỉ lệ % từng mức độ nhận thức |
40 |
30 |
20 |
10 |
|
|
|
|||
D. Bài tập tự luyện
Phần trắc nghiệm
Câu 1. Cho hàm số \(f(x)\) liên tục trên \(R.\) Mệnh đề nào dưới đây đúng ?
A. \(\int{5f(x)\text{d}x}=5\int{f(x)\text{d}x}.\)
B.\(\int{5f(x)\text{d}x}=5+\int{f(x)\text{d}x}.\)
C.\(\int{5f(x)\text{d}x}=\int{f(x)\text{d}x.}\)
D.\(\int{5f(x)\text{d}x}=\frac{1}{5}\int{f(x)\text{d}x.}\)
Câu 2. Mệnh đề nào dưới đây đúng?
A. \(\int{\cos x\text{d}x=\sin x+C.}\)
B. \(\int{\cos x\text{d}x=-\sin x+C.}\)
C. \(\int{\cos x\text{d}x=-\cos x+C.}\)
D. \(\int{\cos x\text{d}x=\frac{1}{2}{{\cos }^{2}}x+C.}\)
Câu 3. Biết \(\int\limits_{2}^{3}{f(x)\text{d}x}=5.\) Giá trị của \(\int\limits_{2}^{3}{5f(x)\text{d}x}\) bằng
A.\(25.\) B.\(10.\) C.\(15.\) D.\(5.\)
Câu 4. Cho \(F(x)\) là một nguyên hàm của hàm số \(f(x)\)trên đoạn \(\left[ a;b \right]\). Mệnh đề nào dưới đây đúng ?
A.\(\int\limits_{a}^{b}{f(x)\text{d}x}=F(b)-F(a).\)
B.\(\int\limits_{a}^{b}{f(x)\text{d}x}=F(a)-F(b).\)
C. \(\int\limits_{a}^{b}{f(x)\text{d}x}=F(b)+F(a).\)
D.\(\int\limits_{a}^{b}{f(x)\text{d}x}=-F(b)-F(a).\)
Câu 5. Cho hàm số \(f(x)\) liên tục và không âm trên đoạn \(\left[ a;b \right].\) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y=f(x)\), trục \(Ox\) và \(2\) đường thẳng \(x=a,x=b\) được tính theo công thức nào dưới đây ?
A. \(S=\int\limits_{a}^{b}{f\left( x \right)}\,\text{d}x.\)
B. \(S=-\int\limits_{a}^{b}{f\left( x \right)}\,\text{d}x.\)
C. \(S=\pi \int\limits_{a}^{b}{{{\left[ f\left( x \right) \right]}^{2}}}\,\text{d}x.\)
D. \(S=\pi \int\limits_{a}^{b}{f\left( x \right)}\,\text{d}x.\)
...
Phần tự luận
Câu 1. Tính tích phân \(I=\int\limits_{0}^{3}{\frac{\text{d}x}{\sqrt{x+1}}}.\)
Câu 2. Trong không gian \(Oxyz,\)viết phương trình đường thẳng \(d\) đi qua điểm \(M(1;2;1)\), đồng thời vuông góc với cả hai đường thẳng \({{\Delta }_{1}}:\frac{x-2}{1}=\frac{y+1}{-1}=\frac{z-1}{1}\) và \({{\Delta }_{2}}:\frac{x+1}{1}=\frac{y-3}{2}=\frac{z-1}{-1}.\)
Câu 3. Tìm tất cả các số phức \(z\) thỏa mãn \(\left| z-1 \right|=\left| 2-5i \right|\).
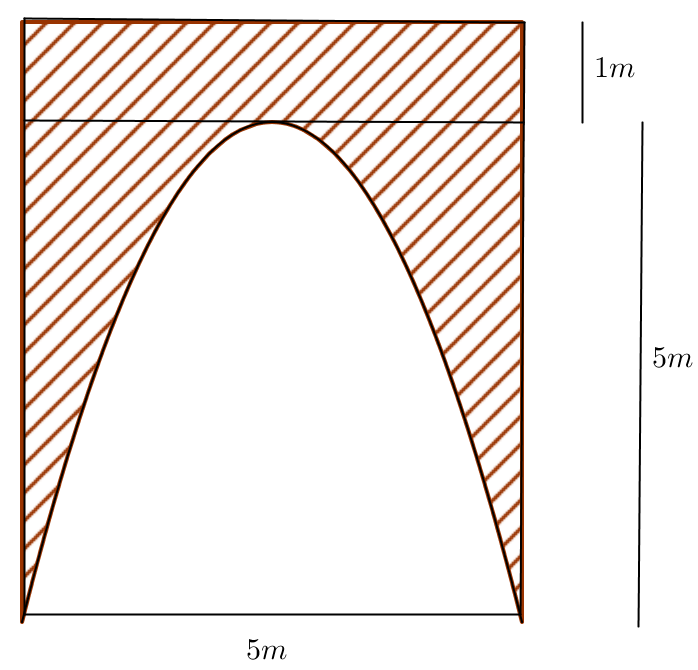
Câu 4. Nhà ông Hải có một cái cổng hình chữ nhật, lối vào cổng có dạng parabol có kích thước như hình vẽ. Ông Hải cần trang trí bề mặt (phần gạch chéo) của cổng. Hỏi ông Hải cần bao nhiêu tiền để trang trí, biết giá thành trang trí là 1.200.000 đồng /1\({{m}^{2}}\)?
-HẾT-
---(Để xem tiếp nội dung của đề cương các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--
Trên đây là một phần trích đoạn nội dung Đề cương ôn tập HK2 môn Toán 12 năm 2022-2023. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.







