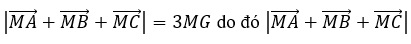Câu hỏi trắc nghiệm (10 câu):
-
Câu 1: Mã câu hỏi: 2358
Tìm khẳng định sai:
- A. Hai vectơ cùng phương với một vectơ thứ ba khác \(\vec{0}\) thì cùng phương
- B. Hai vectơ cùng hướng với một vectơ thứ ba khác \(\vec{0}\) thì cùng phương
- C. Ba vectơ \(\vec{a},\vec{b},\vec{c}\) khác \(\vec{0}\) đôi một cùng phương thì ít nhất có hai vectơ cùng phương
- D. Để \(\vec{a}\) và \(\vec{b}\) bằng nhau thì \(|\vec{a}|=|\vec{b}|\)
-
Câu 2: Mã câu hỏi: 2359
Cho hình bình hành ABCD tâm O. Mệnh đề sai là?
.png)
- A. \(\vec{AB}=\vec{CD}\)
- B. \(\vec{AD}=\vec{BC}\)
- C. \(\vec{AO}=\vec{OC}\)
- D. \(\vec{OD}=\vec{BO}\)
-
Câu 3: Mã câu hỏi: 2360
Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Vectơ \(\vec{CA}-\vec{HC}\) có độ dài là?
.png)
- A. \(\frac{a\sqrt{3}}{2}\)
- B. \(\frac{a\sqrt{5}}{2}\)
- C. \(\frac{a\sqrt{7}}{2}\)
- D. \(\frac{3a}{2}\)
-
Câu 4: Mã câu hỏi: 2361
Cho hình bình hành ABCD có \(AD=2cm, AB=4cm, BD=5cm\). Giá trị của \(|\vec{BA}-\vec{DA}|\) là:
.png)
- A. \(3cm\)
- B. \(4cm\)
- C. \(5cm\)
- D. \(6cm\)
-
Câu 5: Mã câu hỏi: 45010
Cho vectơ \(\overrightarrow a ,\overrightarrow b \) và các số thực m, n, k. Khẳng định nào sau đây là đúng?
- A. Từ đẳng thức ma→=na→ suy ra m = n
- B. Từ đẳng thức ka→=kb→ luôn suy ra a→=b→
- C. Từ đẳng thức ka→=kb→ luôn suy ra k = 0
- D. Từ đẳng thức ma→=na→ và a→≠0→ suy ra m = n
-
Câu 6: Mã câu hỏi: 45011
Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \). Biết rằng B nằm giữa A và C. Giá trị k thỏa mãn điều kiện nào sau đây?
- A. k < 0
- B. k = 1
- C. 0 < k < 1
- D. k > 1
-
Câu 7: Mã câu hỏi: 45012
Cho ba ABC với các trung tuyến AM, BN, CP. Khẳng định nào sau đây sai?
- A. \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \)
- B. \(\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \overrightarrow 0 \)
- C. \(\overrightarrow {CM} + \overrightarrow {CN} + \overrightarrow {AP} = \overrightarrow 0 \)
- D. \(\overrightarrow {AM} + \overrightarrow {AN} + \overrightarrow {AP} = \overrightarrow 0 \)
-
Câu 8: Mã câu hỏi: 45013
Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 2MC. Khi đó khẳng định nào sau đây là đúng?
- A. \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
- B. \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
- C. \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AC} \)
- D. \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
-
Câu 9: Mã câu hỏi: 45014
Cho tam giác ABC và đường thẳng d. Vị trí của điểm M trên d sao cho
có giá trị nhỏ nhất là:
- A. Hình chiếu vuông góc của A trên d
- B. Hình chiếu vuông góc của B trên d
- C. Hình chiếu vuông góc của C trên d
- D. Hình chiếu vuông góc của G trên d, với G là trọng tâm tam giác ABC
-
Câu 10: Mã câu hỏi: 45015
Cho tứ giác ABCD; X là trọng tâm của tam giác BCD, G là trọng tâm tứ giác ABCD. Khẳng định nào sau đây đúng?
- A. \(\overrightarrow {GA} + \overrightarrow {GX} = \overrightarrow 0 \)
- B. \(\overrightarrow {GA} +3 \overrightarrow {GX} = \overrightarrow 0 \)
- C. \(\overrightarrow {GB} + \overrightarrow {GX} = \overrightarrow 0 \)
- D. \(\overrightarrow {GC} + \overrightarrow {GX} = \overrightarrow 0 \)