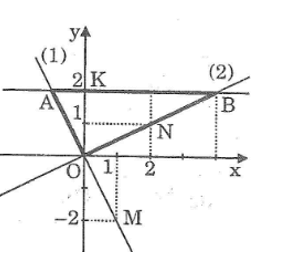
Bài tập 27 trang 68 SBT Toán 9 Tập 1
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số:
y = x (1)
y = 0,5x (2)
b) Đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại điểm C có tung độ bằng 2, theo thứ tự cắt các đường thẳng (1) và (2) tại D và E. Tìm tọa độ của các điểm D, E. Tính chu vi và diện tích tam giác ODE.
Hướng dẫn giải chi tiết
a. *Vẽ đồ thị hàm số y = x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 1 thì y = 1. Ta có: A(1; 1)
Đồ thị hàm số y = x đi qua O và A.
*Vẽ đồ thị hàm số y = 0,5x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 2 thì y = 1. Ta có: B(2; 1)
Đồ thị hàm số y = 0,5x đi qua O và B.
b. Qua điểm C trên trục tung có tung độ bằng 2, kẻ đường thẳng song song với Ox cắt đồ thị hàm số y = x tại D, cắt đồ thị hàm số y = 0,5x tại E.
Điểm D có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = x ta được x = 2.
Vậy điểm D(2; 2)
Điểm E có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = 0,5x ta được x = 4
Vậy điểm E(4; 2)
Gọi D’ và E’ lần lượt là hình chiếu của D và E trên Ox.
Ta có: OD’ = 2, OE’ = 4
Áp dụng định lí Pi-ta-go vào tam giác vuông ODD’, ta có:
OD2 = OD’2 + DD’2 = 22 + 22 = 8
Suy ra: OD = √8 = 2√2
Áp dụng định lí Pi-ta-go vào tam giác vuông OEE’, ta có:
OE2 = OE’2 + EE’2= 42 + 22 = 20
Suy ra: OE = √20 = 2√5
Lại có: DE = CE – CD = 4 – 2 = 2
Chu vi tam giác ODE bằng: OD + DE + EO = 2√2 + 2 + 2√5
= 2(√2 + 1 + √5 )
Diện tích tam giác ODE bằng: 1/2.DE.OC = 1/2.2.2 = 2
-- Mod Toán 9 HỌC247
-


Tìm a và b?
bởi Bùi Đức Tiến
 07/04/2020
07/04/2020
Tìm a và b để đường thẳng (d): y=ax +b đi qua điểm A(1;3) và B(-1;-1), khi đó hãy vẽ đường thẳng d trên hệ trục oxy?
Theo dõi (0) 1 Trả lời -


Tìm hệ số góc của đường thẳng y=ax+b
bởi Trịnh Ánh Tuyết
 05/04/2020
05/04/2020
tìm hệ số góc của đường thẳng y=ã+b(a khác 0) biết đths của hs cắt trục tung tại ddiemr có tung độ bằng 2 và cắt trục hoành tại điểm có hoành độ bằng -3
Theo dõi (1) 0 Trả lời -


Cho hàm số y=2x +1 có đồ thị là đường thẳng (d). Tính góc tạo bởi đường thẳng (d) và trục Ox.
bởi Lan Nguyễn
 03/04/2020
Câu4 : cho h/s y=2x 1 có đồ thị là đường thẳng (d)a) tính góc tạo bởi đường thẳng (d) và trục Ox b) tìm giá trị của m để đường thẳng y=(m-1)×x 2 cắt đường thẳng (d) tại một điểm trên trục hoànhTheo dõi (1) 3 Trả lời
03/04/2020
Câu4 : cho h/s y=2x 1 có đồ thị là đường thẳng (d)a) tính góc tạo bởi đường thẳng (d) và trục Ox b) tìm giá trị của m để đường thẳng y=(m-1)×x 2 cắt đường thẳng (d) tại một điểm trên trục hoànhTheo dõi (1) 3 Trả lời -


Rút gọn biểu thức A = ( 1/1- căn a - 1/1 +căn × ( 1- 1/a) và tính giá trị của A khi a=1/4.
bởi Lan Trần Thị Ngọc
 02/04/2020
Cho biểu thức : A = ( 1/1- căn a - 1/1 căn a) × ( 1- 1/a) a) Rút gọn biểu thức trên b) Tính giá trị của A khi a=1/4
02/04/2020
Cho biểu thức : A = ( 1/1- căn a - 1/1 căn a) × ( 1- 1/a) a) Rút gọn biểu thức trên b) Tính giá trị của A khi a=1/4 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Cho hàm số (d) y= 3x +m a. Xác định m để đường thẳng (d) đi qua gốc tọa độ.
bởi Nít Lương
 30/03/2020
Cho hàm số (d) y= 3x m a, xác định m để đường thẳng (d) đi qua gốc tọa độ. b,tìm m để đường thẳng (d) đi qua A(3;4) . vẽ đồ thị với m vừa tìm được . C, tìm tọa độ giao điểm của đường thẳng vừa vẽ với đường thẳng (d') y=-x 3. D, tính số đo góc taok bởi đường thẳng (d') với trục Ox
30/03/2020
Cho hàm số (d) y= 3x m a, xác định m để đường thẳng (d) đi qua gốc tọa độ. b,tìm m để đường thẳng (d) đi qua A(3;4) . vẽ đồ thị với m vừa tìm được . C, tìm tọa độ giao điểm của đường thẳng vừa vẽ với đường thẳng (d') y=-x 3. D, tính số đo góc taok bởi đường thẳng (d') với trục Ox Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Điều kiện ác định của biểu thức P=căn(2018/(x-2019))
bởi De Hưng
 22/02/2020
22/02/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính góc tạo bởi đường thẳng (d') với trục Ox
bởi Hana Nguyễn
 10/12/2019
Cho (d): y=-x/2 (d): y=2x-1 Tính góc tạo bởi đường thẳng (d') với trục OxTheo dõi (0) 0 Trả lời
10/12/2019
Cho (d): y=-x/2 (d): y=2x-1 Tính góc tạo bởi đường thẳng (d') với trục OxTheo dõi (0) 0 Trả lời