Giải bài 27 tr 20 sách GK Toán 9 Tập 2
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhật hai ẩn rồi giải:
a) \(\left\{\begin{matrix} \frac{1}{x} - \frac{1}{y} = 1& & \\ \frac{3}{x} + \frac{4}{y} = 5& & \end{matrix}\right.\). Hướng dẫn. Đặt \(u=\frac{1}{x};v=\frac{1}{y}\)
b) \(\left\{\begin{matrix} \frac{1}{x - 2} + \frac{1}{y -1} = 2 & & \\ \frac{2}{x - 2} - \frac{3}{y - 1} = 1 & & \end{matrix}\right.\). Hướng dẫn. Đặt \(u=\frac{1}{x-2};v=\frac{1}{y-1}\)
Hướng dẫn giải chi tiết bài 27
Với bài 27 này, chúng ta sẽ biết đổi và đặt ẩn thích hợp sao cho bài toán nhìn "dễ chịu" một chút, có thể giải quyết ra ẩn phụ rồi suy ra nghiệm của phương trình.
Câu a:
Điều kiện: \(x \neq 0;y \neq 0\)
Đặt \(u=\frac{1}{x};v=\frac{1}{y}\), ta được hệ mới là:
\(\left\{\begin{matrix} u-v=1\\ 3u+4v=5 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u=1+v\\ 3(1+v)+4v=5 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u=1+v\\ 7v=2 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u=\frac{9}{7}\\ v=\frac{2}{7} \end{matrix}\right.\)
\(u=\frac{9}{7}\Rightarrow x=\frac{7}{9}\)
\(v=\frac{2}{7}\Rightarrow y=\frac{7}{2}\)
Vậy nghiệm của hệ là \((x;y)=\left (\frac{7}{9};\frac{7}{2} \right )\)
Câu b:
Điều kiện: \(x \neq 2;y \neq 1\)
Đặt \(u=\frac{1}{x-2};v=\frac{1}{y-1}\), ta được hệ mới là:
\(\Leftrightarrow \left\{\begin{matrix} u = 2-v & & \\ 2u - 3v = 1 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u = 2-v & & \\ 2(2-v) - 3v = 1 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u = 2-v & & \\ -5v = -3 & & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} u = \frac{7}{5} & & \\ v = \frac{3}{5} & & \end{matrix}\right.\)
\(u=\frac{7}{5}\Rightarrow \frac{1}{x-2}=\frac{7}{5}\Leftrightarrow x=\frac{19}{7}\)
\(v=\frac{3}{5}\Rightarrow \frac{1}{y-1}=\frac{3}{5}\Leftrightarrow y=\frac{8}{3}\)
Vậy nghiệm của hệ là \((x;y)=\left (\frac{19}{7};\frac{8}{3} \right )\)
-- Mod Toán 9 HỌC247
-


Cho hệ phương trình sau: \(\left\{ \begin{array}{l} {\rm{x}} - 2y = - 3(1)\\ x - y = 3(2) \end{array} \right.\). kết quả của x + y – 1 = ?
bởi Trinh Hung
 21/01/2021
21/01/2021
A. 1
B. – 1
C. 2
D. – 2
Theo dõi (0) 1 Trả lời -


Giải các hệ phương trình sau:
bởi Hoàng Huy Hoàng
 31/07/2020
31/07/2020
Giải giúp mình với đg cần gấp
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


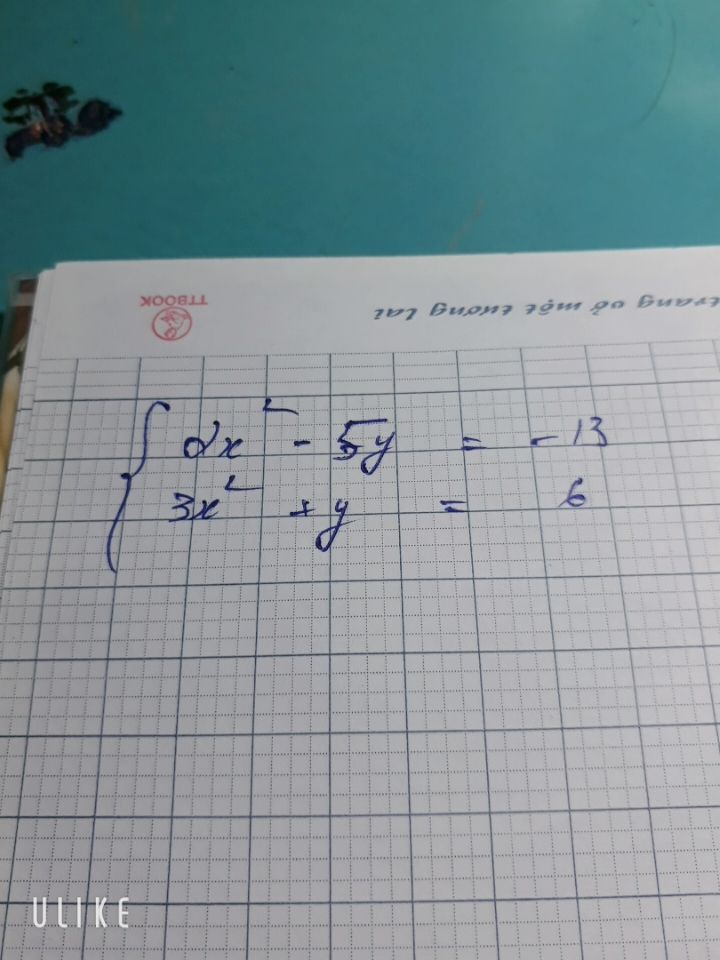
Giải hệ phương trình \(\left\{ \begin{array}{l} 2{x^2} - 5y = - 13\\ 3{x^2} + y = 6 \end{array} \right.\)?
bởi Nguyen Hang Hang
 29/06/2020
29/06/2020
Giải giúp mk bài này ạ
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình \(\left\{ \begin{array}{l} 2\sqrt x + 3\left| {y - 1} \right| = 13\\ - \sqrt x + 2\left| {y - 1} \right| = 4 \end{array} \right.\)?
bởi Anth Thơ
 28/06/2020
28/06/2020
Câu 3
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải hệ phương trình \(\left\{ \begin{array}{l} xy = 5\\ \frac{{y + 2}}{{2x - 1}} + \frac{{2x - 1}}{{y + 2}} = 2 \end{array} \right.\)?
bởi Trang Phạm Thu
 14/06/2020
14/06/2020
Các bn giải giúp mk câu hệ 3) vs mơn các bn nhá
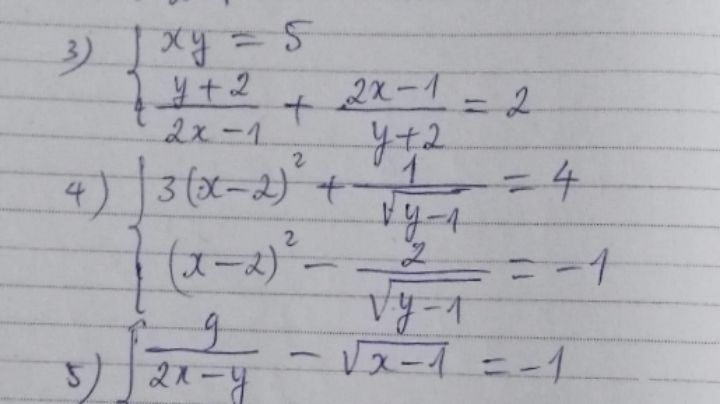 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nghiệm của hệ phương trình sau \(\left\{ \begin{array}{l} \frac{1}{x} + \frac{3}{{2y + 1}} = 2\\ \frac{2}{x} + \frac{4}{{2y + 1}} = 3 \end{array} \right.\)?
bởi Thúi Mắm
 23/05/2020
23/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải hệ phương trình 1/x-1/y=1 và 3/x-4/y=5
bởi Yi Phan
 10/05/2020
Giải giúp mk bt 2 và 4 vs ạ
10/05/2020
Giải giúp mk bt 2 và 4 vs ạ Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải hệ phương trình khi m = 1?
bởi Bin Ni
 24/04/2020
24/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình mx+4y=20 và x+my=10 khi m=3
bởi Kim Thị Duyên
 20/04/2020
20/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nghiệm của hệ phương trình 2x+y=1 và x-y=5
bởi Pham Tuan
 19/04/2020
Cau 14 , 15
19/04/2020
Cau 14 , 15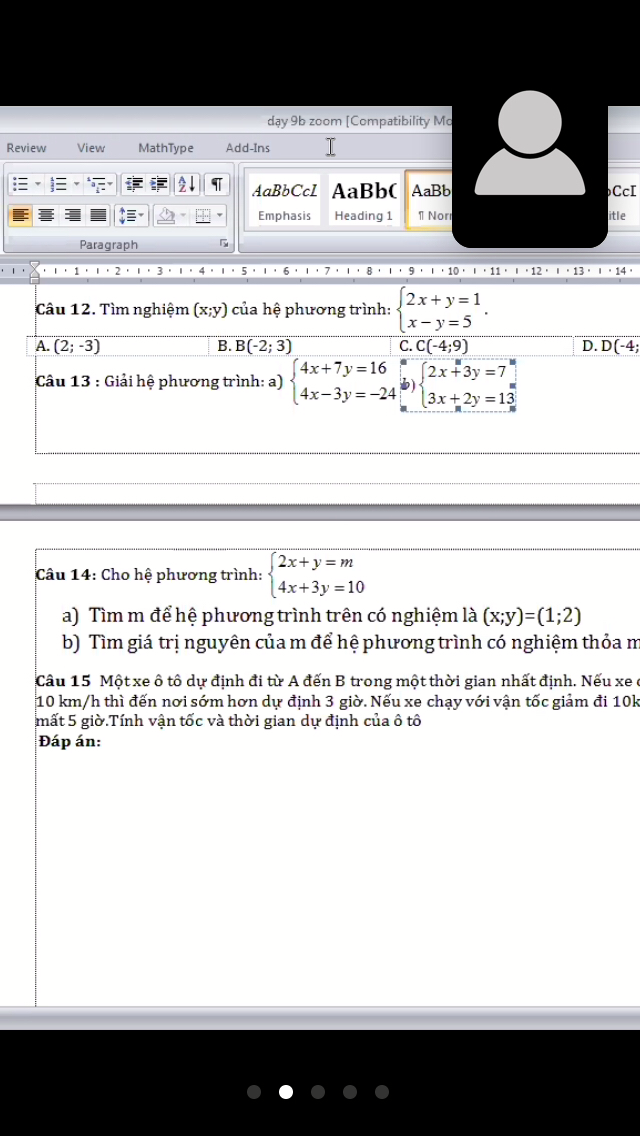 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời -


Giải hệ phương trình x+2y=x và 4x+5y=6
bởi Minh Thư Nguyễn
 12/04/2020
12/04/2020
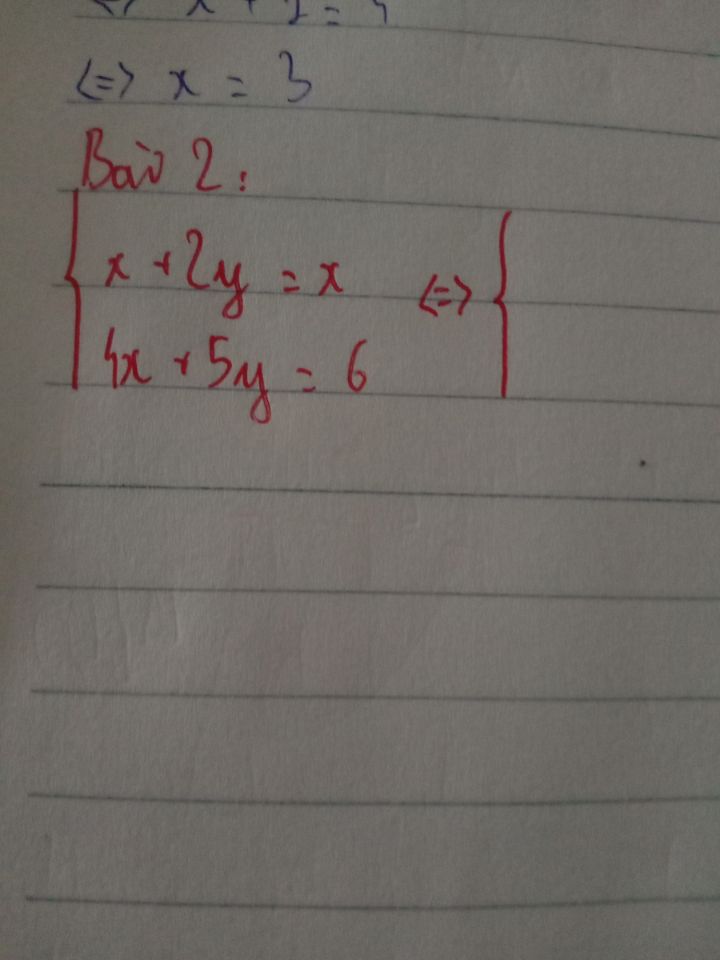 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 25 trang 19 SGK Toán 9 Tập 2
Bài tập 26 trang 19 SGK Toán 9 Tập 2
Bài tập 25 trang 11 SBT Toán 9 Tập 2
Bài tập 26 trang 11 SBT Toán 9 Tập 2
Bài tập 27 trang 11 SBT Toán 9 Tập 2
Bài tập 28 trang 11 SBT Toán 9 Tập 2
Bài tập 29 trang 11 SBT Toán 9 Tập 2
Bài tập 30 trang 11 SBT Toán 9 Tập 2
Bài tập 31 trang 12 SBT Toán 9 Tập 2
Bài tập 32 trang 12 SBT Toán 9 Tập 2
Bài tập 33 trang 12 SBT Toán 9 Tập 2
Bài tập 34 trang 12 SBT Toán 9 Tập 2
Bài tập 4.1 trang 12 SBT Toán 9 Tập 2





