Giải bài 40 tr 34 sách BT Toán lớp 8 Tập 1
Tìm Q, biết :
a. \({{x - y} \over {{x^3} + {y^3}}}.Q = {{{x^2} - 2xy + {y^2}} \over {{x^2} - xy + {y^2}}}\)
b. \({{x + y} \over {{x^3} - {y^3}}}.Q = {{3{x^2} + 3xy} \over {{x^2} + xy + {y^2}}}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng:
+) Thừa số chưa biết \(=\) Tích : thừa số đã biết.
+) Áp dụng quy tắc chia hai phân thức :
\( \dfrac{A}{B} : \dfrac{C}{D} = \dfrac{A}{B}. \dfrac{D}{C}\) với \( \dfrac{C}{D} ≠ 0\).
Lời giải chi tiết
a. \({{x - y} \over {{x^3} + {y^3}}}.Q = {{{x^2} - 2xy + {y^2}} \over {{x^2} - xy + {y^2}}}\)
\(\eqalign{ & \Rightarrow Q = {{{x^2} - 2xy + {y^2}} \over {{x^2} - xy + {y^2}}}:{{x - y} \over {{x^3} + {y^3}}} = {{{{\left( {x - y} \right)}^2}} \over {{x^2} - xy + {y^2}}}.{{{x^3} + {y^3}} \over {x - y}} \cr & Q = {{{{\left( {x - y} \right)}^2}\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)} \over {\left( {{x^2} - xy + {y^2}} \right)\left( {x - y} \right)}} = \left( {x - y} \right)\left( {x + y} \right) = {x^2} - {y^2} \cr} \)
b. \({{x + y} \over {{x^3} - {y^3}}}.Q = {{3{x^2} + 3xy} \over {{x^2} + xy + {y^2}}}\)
\(\eqalign{ & \Rightarrow Q = {{3{x^2} + 3xy} \over {{x^2} + xy + {y^2}}}:{{x - y} \over {{x^3} - {y^3}}} = {{3{x^2} + 3xy} \over {{x^2} + xy + {y^2}}}.{{{x^3} - {y^3}} \over {x - y}} \cr & Q = {{3x\left( {x + y} \right)\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)} \over {\left( {{x^2} + xy + {y^2}} \right)\left( {x + y} \right)}} = 3x\left( {x - y} \right) = 3{x^2} - 3xy \cr} \)
-- Mod Toán 8 HỌC247
-


Tìm phân thức nghịch đảo của phân thức sau: \(\eqalign{ & \,\,{{{x^2} + x - 6} \over {2x + 1}} \cr} \)
bởi Huong Giang
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -


Tìm phân thức nghịch đảo của phân thức sau: \(\eqalign{ & \,\, - {{3{y^2}} \over {2x}} \cr} \)
bởi Hoàng Anh
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -


Làm tính nhân phân thức: \(\dfrac{{{x^3} + 5}}{{x - 7}}.\dfrac{{x - 7}}{{{x^3} + 5}}\)
bởi Phạm Khánh Linh
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -


Cho \(\frac{a}{{b + c}} = \frac{b}{{c + a}} = \frac{c}{{a + b}}\). Chứng minh a=b=c?
bởi lê huy
 24/07/2020
24/07/2020
a/b+c=b/c+a=c/a+b
chứng minh a=b=c
Theo dõi (0) 7 Trả lời -


Tìm GTNN của A?
bởi Lê Nhân
 21/07/2020
21/07/2020
Cho x, y là 2 số thực thỏa x + y=1 . Tìm GTNN của A = x3+ y3 + xy + 1
Theo dõi (0) 10 Trả lời -


So sánh a+5 và b+5 biết a
bởi Mai Anh Đào
 28/04/2020
28/04/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Thực hiện phép tính:
bởi Tiên Võ
 07/04/2020
07/04/2020
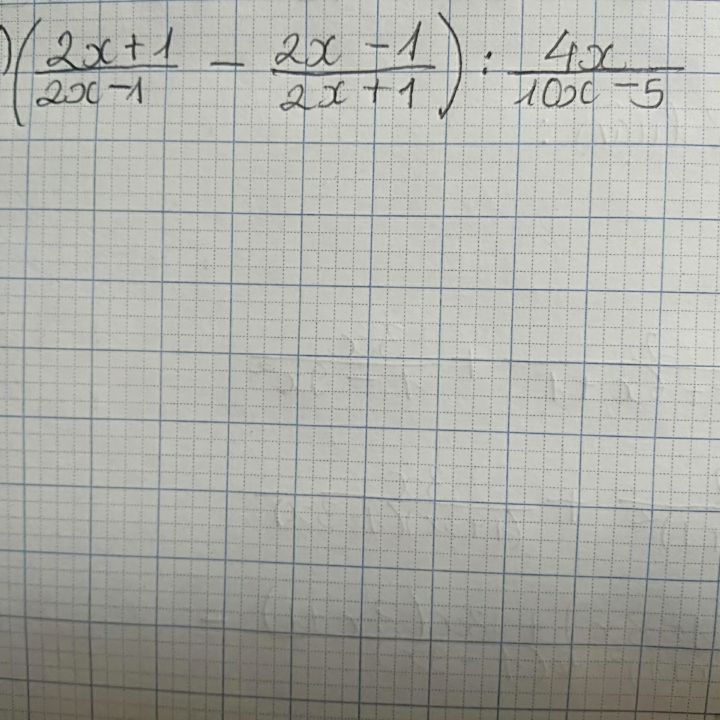 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm điều kiện xác định và rút gọn P?
bởi Hương Giang
 06/04/2020
06/04/2020
Làm giúp mình câu 3 ạ
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời





