Vận dụng trang 19 SGK Toán 11 Chân trời sáng tạo tập 1
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.
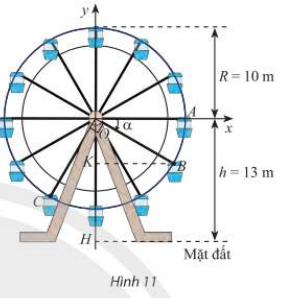
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng \(\left( {13 + 10\sin \alpha } \right)\) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi \(\alpha = - 30^\circ \)
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.
Hướng dẫn giải chi tiết Vận dụng trang 19
Phương pháp giải:
Dựa vào kiến thức lượng giác đã học để tính.
Lời giải chi tiết:
a) Chiều ca từ điểm B đến mặt đất là độ dài đoạn KH
Ta có: \(KH = OH - OK = 13 - OB.\cos \left( {\frac{\pi }{2} - \alpha } \right) = 13 - 10.\sin \left( { - \alpha } \right) = 13 + 10.\sin \alpha \)
Với \(\alpha = - 30^\circ \Rightarrow KH = 13 + 10.\sin \left( { - 30^\circ } \right) = 8\,\,\left( m \right)\)
b) Nếu B cách mặt đất 4m \( \Rightarrow 4 = 13 + 10\sin \alpha \Leftrightarrow \sin \alpha = - \frac{9}{{10}}\)
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( { - \frac{9}{{10}}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = - \frac{{\sqrt {19} }}{{10}}\)
Gọi M là hình chiếu của C lên OH
\( \Rightarrow \cos \left( {\widehat {COH}} \right) = \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha = - \frac{{\sqrt {19} }}{{10}}\)
Mà \(\cos \widehat {COH} = \frac{{OM}}{{OC}} \Rightarrow - \frac{{\sqrt {19} }}{{10}} = \frac{{OM}}{{OC}} \Rightarrow OM \approx 4,36\,\,\left( m \right)\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động khám phá 3 trang 17 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 7 trang 20 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 8 trang 20 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 51 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 11 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST





