Hoạt động khám phá 3 trang 17 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

Phương pháp giải:

Vẽ đường tròn lượng giác dựa vào kiến thức đã học rồi nhận xét.

Lời giải chi tiết:

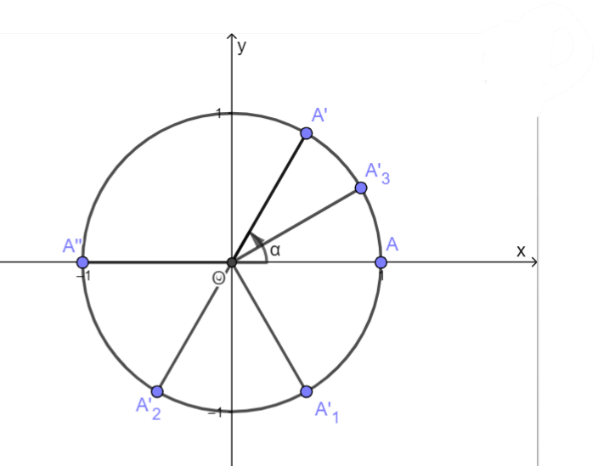
Dựa vào đường tròn lượng giác ta nhận được:

\(\left. \begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}tan\left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array} \right.\)

\(\left. \begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array} \right.\)

\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\pi - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\pi - \frac{\pi }{3}} \right) = - \frac{1}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\\\cos \left( {\pi - \frac{\pi }{3}} \right) = - \cos \frac{\pi }{3}\end{array} \right. \\
\Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)

\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \frac{1}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \cos \frac{\pi }{3}\\\cos \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array} \right.\end{array}\)

-- Mod Toán 11 HỌC247