Hoạt động khám phá 3 trang 73 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:

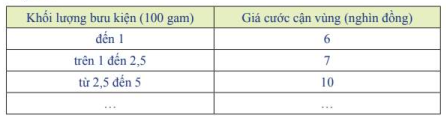
Nếu chỉ xét trên khoảng từ 0 đến 5 (tính theo 100 gam) thì hàm số giả cước (tính theo nghìn đồng) xác định như sau:

\(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}6&{khi\,\,x \in \left( {0;1} \right]}\\7&{khi\,\,x \in \left( {1;2,5} \right]}\\{10}&{khi\,\,x \in \left( {2,5;5} \right]}\end{array}} \right.\)

Đồ thị của hàm số như Hình 2.

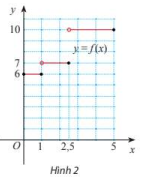
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì sao cho \(x \in \left( {1;2,5} \right)\) và \(\lim {x_n} = 1\). Tìm \(\lim f\left( {{x_n}} \right)\).

b) Giả sử \(\left( {{x_n}'} \right)\) là dãy số bất kì sao cho \({x_n}' \in \left( {0;1} \right)\) và \(\lim {x_n}' = 1\). Tìm \(\lim f\left( {{x_n}'} \right)\).

c) Nhận xét về kết quả ở a) và b)