Hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 4 Bài 3 Đường thẳng và mặt phẳng song song môn Toán lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 107 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Đường thẳng a trên mép hiên của tòa nhà có điểm nào chung với mặt (P) của phố đi bộ Nguyễn Huệ không?

-
Hoạt động khám phá 1 trang 107 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hai hình bình hành \(ABCD\) và \(ABMN\) không đồng phẳng. Tìm số giao điểm của mặt phẳng \(\left( {ABCD} \right)\) lần lượt với các đường thẳng \(MN,MA\) và \(AC\).
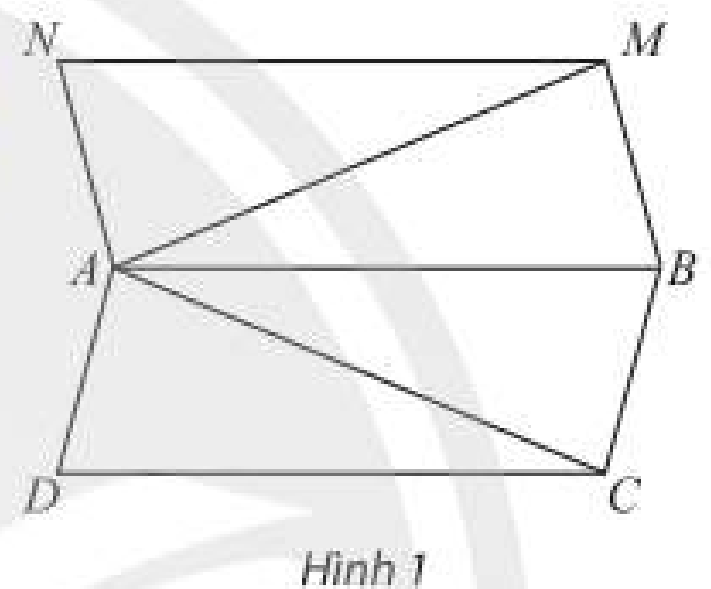
-
Thực hành 1 trang 108 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho \(E\) và \(F\) lần lượt là trung điểm các cạnh \(AB\) và \(AC\) của tứ diện \(ABC{\rm{D}}\). Xác định vị trí tương đối của các đường thẳng \(BC,AD\) và \(EF\) với mặt phẳng \(\left( {BCD} \right)\).
-
Hoạt động khám phá 2 trang 108 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và \(a\) song song với một đường thẳng \(b\) nằm trong \(\left( P \right)\). Đặt \(\left( Q \right) = mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Giả sử \(a\) có điểm chung \(M\) với \(\left( P \right)\) thì điểm \(M\) phải nằm trên đường thẳng nào? Điều này có trái với giả thiết \(a\parallel b\) hay không?
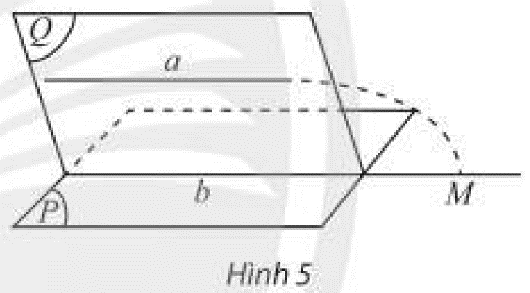
-
Thực hành 2 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hình chóp \(S.ABC\) có \(A',B',C'\) lần lượt là trung điểm của \(SA,SB,SC\). Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng \(\left( {ABC} \right)\).
-
Vận dụng 1 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hãy chỉ ra trong Hình 9 các đường thẳng lần lượt nằm trong, song song, cắt mặt phẳng sàn nhà.

-
Hoạt động khám phá 3 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
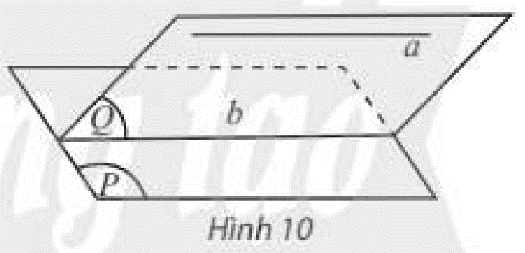
-
Hoạt động khám phá 4 trang 110 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hai đường thẳng chéo nhau \(a,b\). Lấy một điểm \(M\) trên \(a\), vẽ đường thẳng \(b'\) đi qua \(M\) và song song với \(b\). Đặt \(\left( P \right)\) là mặt phẳng đi qua \(a,b'\).
a) Có nhận xét gì về mối liên hệ giữa \(b\) và \(\left( P \right)\).
b) Gọi \(\left( {P'} \right)\) là mặt phẳng chứa \(a\) và song song với \(b\). Có nhận xét gì về mối liên hệ giữa \(b'\) và \(\left( {P'} \right)\); \(\left( P \right)\) và \(\left( {P'} \right)\)?
-
Thực hành 3 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,E\) lần lượt là trung điểm của các đoạn thẳng \(AB,CD,SA\) (Hình 17). Chứng minh rằng:
a) \(MN\) song song với hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\);
b) \(SB\) và \(SC\) song song với mặt phẳng \(\left( {MNE} \right)\).
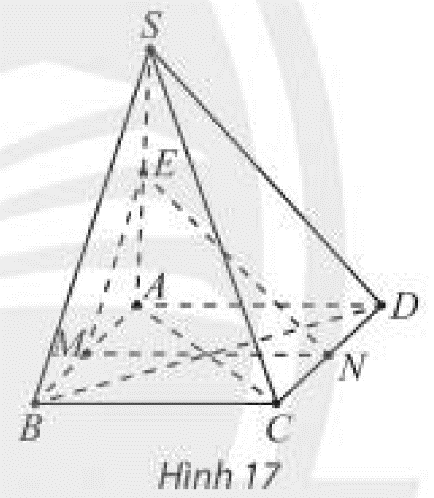
-
Vận dụng 2 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Làm thế nào để đặt cây thước kẻ a để nó song song các trang của một cuốn sách?
-
Giải Bài 1 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm hai đường chéo. Cho \(M\) là trung điểm của \(SC\).
a) Chứng minh đường thẳng \(OM\) song song với hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBA} \right)\);
b) Tìm giao tuyến của hai mặt phẳng \(\left( {OMD} \right)\) và \(\left( {SAD} \right)\).
-
Giải Bài 2 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của \(ABCD\) và \(ABEF\).
a) Chứng minh đường thẳng \(OO'\) song song với các mặt phẳng \(\left( {CDF{\rm{E}}} \right),\left( {ADF} \right)\) và \(\left( {BCE} \right)\).
b) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AF\) và \(BE\). Chứng minh \(MN\parallel \left( {CDF{\rm{E}}} \right)\).
c) Tìm giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\).
-
Giải Bài 3 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và một điểm \(M\) di động trên cạnh \(AD\). Một mặt phẳng \(\left( \alpha \right)\) qua \(M\), song song với \(C{\rm{D}}\) và \(SA\), cắt \(BC,SC,SD\) lần lượt tại \(N,P,Q\).
a) \(MNPQ\) là hình gì?
b) Gọi \(I = MQ \cap NP\). Chứng minh rằng \(I\) luôn luôn thuộc một đường thẳng cố định khi \(M\) di động trên \(AD\).
-
Giải Bài 4 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?
-
Giải Bài 5 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB\). Gọi \(M\) là trung điểm của \(CD\), \(\left( P \right)\) là mặt phẳng qua \(M\) song song với \(SA\) và \(BC\). Tìm giao tuyến của \(\left( P \right)\) với các mặt của hình chóp \(S.ABCD\).
-
Giải Bài 6 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Mô tả vị trí tương đối của các đường thẳng \(a,b,c,d,e\) với mặt phẳng \(\left( P \right)\) là mặt trước của toà nhà (Hình 19).

-
Bài tập 1 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác ABD và ACD. Chứng minh G1G2 song song với các mặt phẳng (ABC) và (BCD)?
-
Bài tập 2 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.
a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho AM = AF, AN = AD Chứng minh MN // (DCEF).
-
Bài tập 3 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi G là trọng tâm của tam giác SAB, I là trung điểm của AB và M là điểm thuộc cạnh AD sao cho AM = AD. Đường thẳng đi qua M và song song với AB cắt CI tại N. Chứng minh:
a) NG // (SCD);
b) MG // (SCD).
-
Bài tập 4 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh:
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP).
d) Gọi G1 và G2 theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh G1G2 song song với (SAD).
-
Bài tập 5 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi (α) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng (α) với các mặt của hình chóp?






