Bài tập 5 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi (α) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng (α) với các mặt của hình chóp?
Hướng dẫn giải chi tiết Bài tập 5
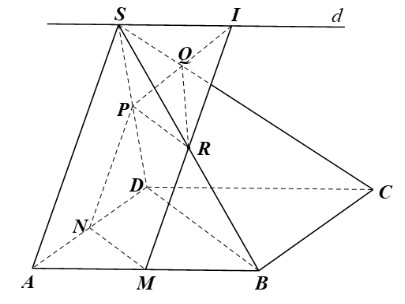
Gọi N, P, R lần lượt là trung điểm của AD, SD, SB.
Xét ∆ABD có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác.
Do đó MN // BD.
Xét ∆SBD có P, R lần lượt là trung điểm của SD, SB nên PR là đường trung bình của tam giác.
Do đó PR // BD.
Từ các kết quả trên ta có: MN // PR (do cùng song song với BD).
Suy ra bốn điểm M, N, P, R tạo thành một mặt phẳng (MNPR).
Ta có MN // BD và MN ⊂ (MNPR) nên BD // (MNPR)
Tương tự, ta cũng có SA // (MNPR)
Ta thấy (MNPR) đi qua M và song song với BD, và SA nên chính là mp(α).
Trong mặt phẳng (SAB) vẽ đường thẳng d đi qua S và d // AB // CD.
Khi đó, giả sử MR cắt d tại I, PI cắt SC tại Q.
Lúc này, mặt phẳng (α) là (MNPI).
Ta có MN ⊂ (ABCD), MN ⊂ (MNPI) nên (MNPI) ∩ (ABCD) = MN hay (α) ∩ (ABCD) = MN.
Tương tự, (α) ∩ (SAD) = NP, (α) ∩ (SCD) = PQ, (α) ∩ (SBC) = QR, (α) ∩ (SAB) = MR.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





