Bài tập 2 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.
a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho AM = AF, AN = AD Chứng minh MN // (DCEF).
Hướng dẫn giải chi tiết Bài tập 2
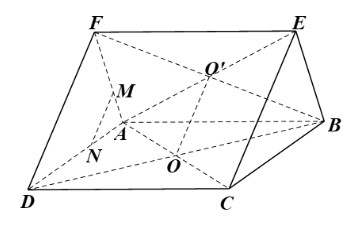
a) Do O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.
Xét trong ∆BDF có: O, O’ lần lượt là trung điểm của BD, BF nên OO’ là đường trung bình của ∆BDF, suy ra OO’ // DF. (1)
Tương tự, trong ∆ACE ta cũng có OO’ // CE. (2)
Từ (1) và (2) suy ra OO’ // DF // CE, mà DF ⊂ (ADF), CE ⊂ (BCE).
Suy ra OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Do AM = AF, AN = AD nên
Xét ∆ADF có suy ra MN // DF. (định lý Thalès đảo)
Mà DF ⊂ (DCEF), suy ra MN // (DCEF).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 6 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST





